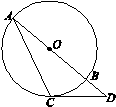
题目内容
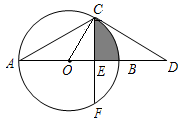
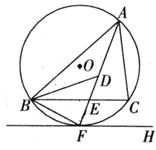
如图,AB为⊙O的直径,点C在⊙O上,点D在AB的延长线上,且AC=CD,已知∠D=30°.
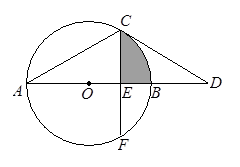
⑴判断CD与⊙O的位置关系,请说明理由
⑵若弦CF⊥AB,垂足为E,且CF=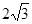 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
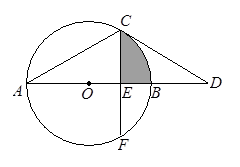
⑴判断CD与⊙O的位置关系,请说明理由
⑵若弦CF⊥AB,垂足为E,且CF=
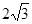 ,求图中阴影部分的面积.
,求图中阴影部分的面积.⑴CD与⊙O相切⑵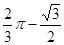
解:(1)CD与⊙O相切 …………… 1分
理由:连接OC …………… 2分
∵AC=DC,
∴∠A=∠D=30°
∵AO=CO,
 ∴∠OCA=∠A=30°∠COD=60°,………… 3分
∴∠OCA=∠A=30°∠COD=60°,………… 3分
∴∠D+∠COD=90°,
∴∠OCD=90°
∴OC⊥CD,
∴CD与⊙O相切………………4分
(2)∵CF⊥AB,∴CE=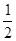 CF=
CF=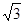 ………… 5分
………… 5分
 在Rt△OCE中,有,sin600=
在Rt△OCE中,有,sin600=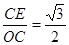 , ∴ OC=2,OE="1" ,
, ∴ OC=2,OE="1" ,
 -
-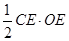
=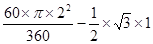 =
=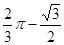 ………… 8分
………… 8分
(1)连接OC,根据题意可求得∠A=30°,则∠OCA=30°,则∠OCD=90°,从而证得CD与⊙O相切;
(2)可求得CE,再在Rt△OCE中,利用三角函数求出OC,OE,即可得出阴影部分的面积
理由:连接OC …………… 2分
∵AC=DC,
∴∠A=∠D=30°
∵AO=CO,
 ∴∠OCA=∠A=30°∠COD=60°,………… 3分
∴∠OCA=∠A=30°∠COD=60°,………… 3分∴∠D+∠COD=90°,
∴∠OCD=90°
∴OC⊥CD,
∴CD与⊙O相切………………4分
(2)∵CF⊥AB,∴CE=
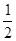 CF=
CF=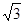 ………… 5分
………… 5分 在Rt△OCE中,有,sin600=
在Rt△OCE中,有,sin600=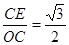 , ∴ OC=2,OE="1" ,
, ∴ OC=2,OE="1" ,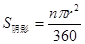 -
-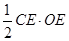
=
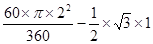 =
=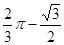 ………… 8分
………… 8分(1)连接OC,根据题意可求得∠A=30°,则∠OCA=30°,则∠OCD=90°,从而证得CD与⊙O相切;
(2)可求得CE,再在Rt△OCE中,利用三角函数求出OC,OE,即可得出阴影部分的面积

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
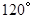 的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是 。
的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是 。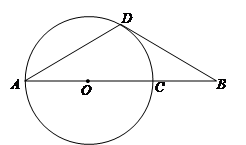
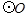 上一点
上一点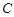 作
作 直径
直径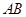 的延长线于点D. 若∠D=40°,则∠A的度数为( )
的延长线于点D. 若∠D=40°,则∠A的度数为( )