题目内容
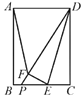
【题目】如图,菱形ABCD的周长为8,对角线BD=2,E、F分别是边AD,CD上的两个动点;且满足AE+CF=2.
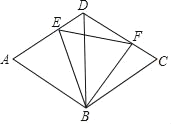
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
【答案】(1)见解析;(2)△BEF是等边三角形.理由见解析
【解析】
(1)先判定△ABD与△BCD都是等边三角形,根据等边三角形的性质可得∠BDE=∠C=60°,再求出DE=CF,然后利用“边边角”证明两三角形全等;
(2)根据全等三角形对应边相等可得BE=CF,全等三角形对应角相等可得∠DBE=∠CBF,然后求出∠EBF=60°,再根据等边三角形的判定得解,利用旋转变换解答.
(1)证明:∵菱形ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2﹣AE,
又∵DE=AD﹣AE=2﹣AE,
∴DE=CF,
在△BDE和△BCF中,
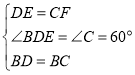 ,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形,
由图可知,△BDE绕点B顺时针旋转60°即可得到△BCF.
故答案为:(1)见解析;(2)△BEF是等边三角形.理由见解析.

【题目】某数学兴趣小组在探究函数y=x2﹣2|x|+3的图象和性质时,经历了以下探究过程:
(1)列表(完成下列表格).
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | 0 |
| 1 | 2 | 3 | … |
y | … | 6 | 3 | 2 |
|
|
| 2 | 3 | 6 | … |
(2)描点并在图中画出函数的大致图象;
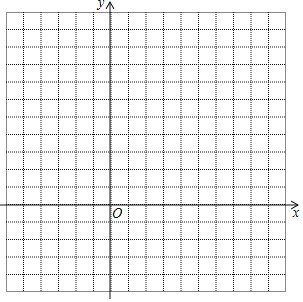
(3)根据函数图象,完成以下问题:
①观察函数y=x2﹣2|x|+3的图象,以下说法正确的有 (填写正确的序号)
A.对称轴是直线x=1;
B.函数y=x2﹣2|x|+3的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2);
C.当﹣1<x<1时,y随x的增大而增大;
D.当函数y=x2﹣2|x|+3的图象向下平移3个单位时,图象与x轴有三个公共点;
E.函数y=(x﹣2)2﹣2|x﹣2|+3的图象,可以看作是函数y=x2﹣2|x|+3的图象向右平移2个单位得到.
②结合图象探究发现,当m满足 时,方程x2﹣2|x|+3=m有四个解.
③设函数y=x2﹣2|x|+3的图象与其对称轴相交于P点,当直线y=n和函数y=x2﹣2|x|+3图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,求n的值.