题目内容
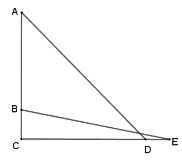
【题目】在某海域,一艘海监船在P处检测到南偏西45°方向的B处有一艘不明船只,正沿正西方向航行,海监船立即沿南偏西60°方向以40海里/小时的速度去截获不明船只,经过1.5小时,刚好在A处截获不明船只,求不明船只的航行速度.(![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数).
≈1.73,结果保留一位小数).
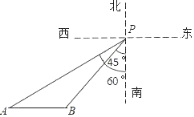
【答案】不明船只的航行速度是14.6海里/小时.
【解析】
作PQ垂直于AB的延长线于点Q,在△APQ和△BQP中,利用三角函数的知识分别求出AQ、BQ长,继而可求得AB长,再根据时间即可求出速度.
作PQ垂直于AB的延长线于点Q,
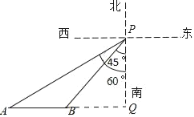
由题意得:∠BPQ=45°,∠APQ=60°,AP=1.5×40=60海里,
∴在△APQ中,AQ=APsin60°=30![]() 海里,PQ=APcos60°=30海里,
海里,PQ=APcos60°=30海里,
∵在△BQP中,∠BPQ=45°,
∴PQ=BQ=30海里,
∴AB=AQ﹣BQ=30![]() ﹣30≈21.9海里,
﹣30≈21.9海里,
∴![]() =14.6海里/小时,
=14.6海里/小时,
∴不明船只的航行速度是14.6海里/小时.

练习册系列答案
相关题目