题目内容
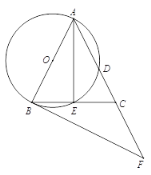
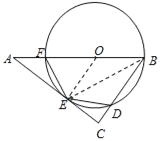
【题目】如图,点O是△ABC的边AB上一点,⊙O与半径AC相切于点E,与边BC、AB分别相交于点D、F,且DE=EF.
⑴求证:∠C=90o;
⑵当BC=2,sinA=![]() 时,求AF的长.
时,求AF的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)如图,连接OE,BE,通过对等弦、对等弧、对等圆周角以及等量转化找到∠OEB与∠DBE相等,再运用切线和平行线的定理即可解答
(2)先求出AB的长度,再通过解Rt△AOE求出半径长度,最后求出AF的长度.
解:(1)连接OE,BE,
∵DE=EF,∴![]() ;
;
∴∠OBE=∠DBE.
∵OE=OB,∴∠OEB=∠OBE.
∴∠OEB=∠DBE.
∴OE∥BC.
∵⊙O与边AC相切于点E,∴OE⊥AC.
∴∠AEO=90°.
∴∠C=∠AEO=90°
(2)在△ABC,∠C=90°,BC=2,sinA=![]() ,∴AB=5.
,∴AB=5.
设⊙O的半径为r,则AO=5﹣r,
在Rt△AOE中,sinA=![]() =
=![]() ,∴r=
,∴r=![]() .
.
∴AF=5﹣2×![]() =
=![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目