题目内容
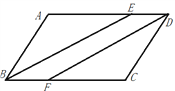
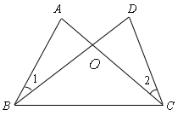
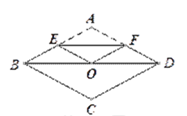
【题目】如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2![]() ,则∠A的度数为____________ .
,则∠A的度数为____________ .
【答案】120°
【解析】分析:
连接AC,根据菱形的性质易得AC⊥BD,由折叠的性质易得EF⊥AC,EF平分AO,由此可得EF∥BD,从而可得EF是△ABD的中位线,由此即可得到BD的长,从而可得BO的长,进而由勾股定理可得AO的长,从而可得∠ABO的度数,由此即可解得∠BAD的度数了.
详解:
连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵A沿EF折叠后与点O重合,
∴EF⊥AC,EF平分AO,
∴EF∥BD,
∴E、F分别是AB、AD的中点,
∴EF是△ABD的中位线,
∴BD=2EF=![]() ,
,
∴BO=![]() ,
,
∴AO=![]() ,
,
∴AO=![]() AB,
AB,
∴∠ABO=30°,
∴∠BAO=60°,
∴∠BAD=120°.
故选A.


 名校课堂系列答案
名校课堂系列答案【题目】在一次社会调查活动中,小李收集到某“健步走运动”团队20名成员一天行走的步数,记录如下:
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8753 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理.

(1)请完成下面频数分布统计表;
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | |
B | 6500≤x<7500 | |
C | 7500≤x<8500 | |
D | 8500≤x<9500 | |
E | 9500≤x<10500 |
(2)在上图中请画出频数分布直方图;
(3)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个.比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分
组别 | 听写正确的个数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
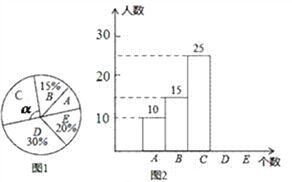
根据以上信息解决下列问题:
(1)本次共随机抽查了多少名学生,求出m,n的值并补全图2的条形统计图;
(2)求出图1中![]() 的度数;
的度数;
(3)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
【题目】如图,AB = 6cm,∠CAB = 25°,P是线段AB上一动点,过点P作PM⊥AB交射线AC于点M,连接MB,过点P作PN⊥MB于点N.设A,P两点间的距离为xcm,P,N两点间的距离为ycm.(当点P与点A或点B重合时,y的值均为0)小海根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.

下面是小海的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0.00 | 0.60 | 1.00 | 1.51 | 2.00 | 2.75 | 3.00 | 3.50 | 4.00 | 4.29 | 4.90 | 5.50 | 6.00 |
y/cm | 0.00 | 0.29 | 0.47 | 0.70 | 1.20 | 1.27 | 1.37 | 1.36 | 1.30 | <>1.00 | 0.49 | 0.00 |
(说明:补全表格时相关数值保留两位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当y=0.5时,与之对应的![]() 值的个数是 .
值的个数是 .