题目内容
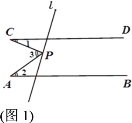
【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
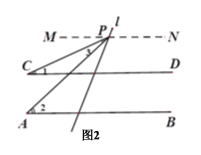
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).


【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() ,理由见解析;(4)
,理由见解析;(4)![]() .
.
【解析】
(1)如图1(见解析),过点P作![]() ,根据平行线的判定可得
,根据平行线的判定可得![]() ,再根据平行线的性质可得
,再根据平行线的性质可得![]() ,然后根据角的和差即可得;
,然后根据角的和差即可得;
(2)用题(1)的方法即可得;
(3)如图2(见解析),过点P作![]() ,根据平行线的判定可得
,根据平行线的判定可得![]() ,再根据平行线的性质可得
,再根据平行线的性质可得![]() ,然后根据角的和差即可得;
,然后根据角的和差即可得;
(4)先根据角平分线的定义、题(3)的结论求出![]() 的度数,再归纳类推出一般规律即可.
的度数,再归纳类推出一般规律即可.
(1)如图1,过点P作![]()
![]()
![]()
![]()
![]() ;
;

(2)结论为![]() ,理由如下:
,理由如下:
如图1,过点P作![]()
![]()
![]()
![]()
![]() ;
;
(3)结论为![]() ,理由如下:
,理由如下:
如图2,过点P作![]()
![]()
![]()
![]()
![]() ;
;
(4)由题意得:![]() 平分
平分![]() ,
,![]() 平分
平分![]() ;
;![]() 平分
平分![]() ,
,![]() 平分
平分![]() ;并且点
;并且点![]() 均在CD的上方
均在CD的上方
由角平分线的定义得:![]()
由(3)的结论得:![]()
同理可得:![]()
归纳类推得:![]() .
.

练习册系列答案
相关题目