题目内容
【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,过点D作BE的平行线交于BC于F.
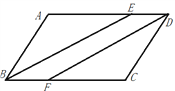
(1)求证:△ABE≌△CDF;
(2)若AB=6,BC=8,求DE的长.
【答案】(1)证明见解析(2)2
【解析】(1)首先由平行四边形的性质可得AD∥BC,AB=CD;∠A=∠C,再由条件利用SAS定理可判定△ABE≌△CDF;(2)由(1)可知 ∠EBF=∠AEB由平行线的性质和角平分线得出∠AEB=∠ABE,即可得出结果.
解:(1)证明:法一:
∵四边形ABCD是平行四边形
∴AD∥BC,AD=BC,∠A=∠C,,
∵BE∥DF,

∴四边形BEDF是平行四边形,
∴DE=BF,
∴AD-DE=BC-BF,
即:AE=CF,
∴△ABE≌△CDF(SAS).
法二:∵BE//FD ∴∠EBF=∠DFC
∵AD//BC ∴∠EBF=∠AEB
∴∠AEB=∠DFC
在ABCD中,∵∠A=∠C,AB=CD
∴ △ABE≌△CDF
(2)由(1)可知 ∠EBF=∠AEB
又∵BE平分∠EBF
∴∠EBF=∠ABE
∴∠AEB=∠ABE
∴AE=AB=6
又∵BC=AD=8
∴DE=2
“点睛”本题考查了平行四边形的判定与性质、等腰三角形的判定;熟记平行四边形的性质,证出AE=AB是解决(2)的关键.

 名校课堂系列答案
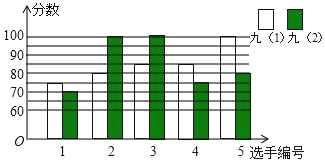
名校课堂系列答案【题目】为选拔优秀选手参加瑶海区第八届德育文化艺术节“诵经典”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示
(1)根据图示填写下表
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 |
| 85 |
九(2) |
| 80 |
|
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班五名选手的成绩较稳定.