题目内容
【题目】如图,在直角坐标系中,直线y=![]() x+1与x轴、y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=﹣x2+bx+c与x轴分别交于点A、C.
x+1与x轴、y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=﹣x2+bx+c与x轴分别交于点A、C.
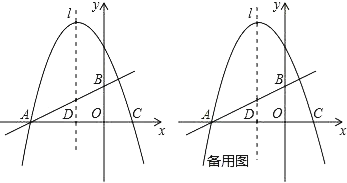
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,设抛物线的对称轴l与x轴交于一点D,连接PD,交AB于E,求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标;
(3)若点Q在第二象限内,且tan∠AQD=2,线段CQ是否存在最小值?如果存在直接写出最小值,如果不存在,请说明理由.
【答案】(1)y=﹣x2﹣2x+3;(2)点P的坐标是(﹣1,4)或(﹣2,3);(3)存在,CQ的最小值为![]() -
-![]() .
.
【解析】
(1)利用对称性和待定系数法求函数关系式;
(2)分类讨论三角形相似情况即可;
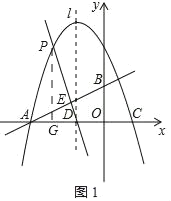
(3)由已知,满足条件的Q点在以A、D、F(﹣1,1)的圆E在第二象限的部分,连接CE交圆于Q,则CQ最小.
解:(1)∵直线y=![]() x+1与x轴交点为A,
x+1与x轴交点为A,
∴点A的坐标为(﹣3,0),
∵抛物线的对称轴为x=﹣1,
∴点C的坐标为(1,0),
∵抛物线y=﹣x2+bx+c与x轴分别交于点A、C,
∴抛物线为y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3;
(2)∵抛物线y=﹣x2﹣2x+3的对称轴为x=﹣1,
∴点D的坐标为(﹣1,0),
①当∠ADE=90°时,△ADE∽△AOB.此时点P在对称轴上,即点P为抛物线的顶点,坐标为(﹣1,4);
②当∠AED=90°时,△AED∽△AOB.
过点P作PG⊥AC于点G,则△AED∽△PGD.
于是![]() =
=![]() =
=![]() =
=![]() ,
,
∴PG=3GD.
即:﹣t2﹣2t+3=3(﹣1﹣t),
解得 t1=﹣2,t2=3(不合题意,舍去).
当t=﹣2时,﹣22+2×2+3=3,
所以此时点P的坐标为(﹣2,3).
综上所述,点P的坐标是(﹣1,4)或(﹣2,3);
(3)存在,CQ的最小值为![]() ﹣
﹣![]() ,
,

如图,取点F(﹣1,1),过点ADF作圆,则点E(﹣2,![]() )为圆心.
)为圆心.
∵tan∠AFD=2,
∴圆弧AFD(A、D除外)上的点都是满足条件的Q点.
连CE交⊙E于点Q,则CQ为满足条件的最小值,
此时CE=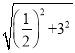 =
=![]() ,⊙E半径为
,⊙E半径为![]() ,
,
∴CQ最小值为![]() ﹣
﹣![]() .
.
故答案为:(1)y=﹣x2﹣2x+3;(2)点P的坐标是(﹣1,4)或(﹣2,3);(3)存在,CQ的最小值为![]() -
-![]() .
.