题目内容
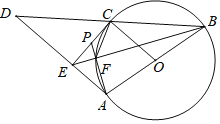
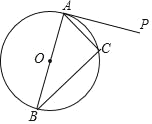
【题目】如图所示,以BC为直径的⊙O中,点A、E为圆周上两点,过点A作AD⊥BC,垂足为D,作AF⊥CE的延长线于点F,垂足为F,连接AC、AO,已知BD=EF,BC=4.
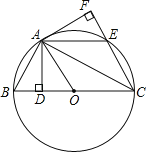
(1)求证:∠ACB=∠ACF;
(2)当∠AEF= °时,四边形AOCE是菱形;
(3)当AC= 时,四边形AOCE是正方形.
【答案】(1)见解析;(2)60;(3)![]() .
.
【解析】
(1)证明△ABD≌△AEF,可得AB=AE,则结论得证;
(2)根据菱形的判定方法,当OC=CE=AE=OA时,四边形OAEC为菱形,则可判断△OCE为等边三角形,所以∠OCE=60°,可得∠AEF=60°;
(3)利用正方形的判定方法,当∠AOC=90°时,四边形AOCE为正方形,则根据正方形的性质计算出此时AC的长.
解:(1)证明:∵∠ABC+∠AEC=∠AEC+∠AEF=180°,
∴∠ABC=∠AEF,
在△ABD和△AEF中, ,
,
∴△ABD≌△AEF(ASA)
∴AB=AE,
∴∠ACB=∠ACF;
(2)60,
如图所示,连接OE,
∵四边形AOCE是菱形,
∴OA=OC=CE=AE,
∵OC=CE=OE,
∴△ECO是等边三角形,
∴∠OCE=60°,
∴AE∥BC,
∴∠AEF=∠OCE=60°.
故答案为:60;
(3)∵BC=4,
∴OC=![]() =2,
=2,
∵四边形AOCE是正方形,
∴∠AOC=90°,
∴![]() .
.
故答案为:![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
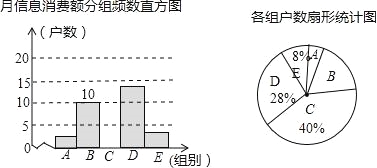
综合自测系列答案【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?