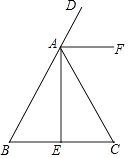题目内容
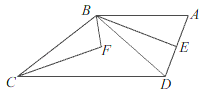
【题目】如图，已知四边形ABCD中，AB∥DC，连接BD，BE平分∠ABD，BE⊥AD，∠EBC和∠DCB的角平分线相交于点F，若∠ADC=110°，则∠F的度数为（ ）
A. 115° B. 110° C. 105° D. 100°
【答案】D
【解析】
依据四边形BCDE的内角和，可得∠BCD+∠CBE=160°，再根据∠EBC和∠DCB的角平分线相交于点F，可得∠BCF+∠CBF=
×160°=80°，进而得出△BCF中，∠F=180°-80°=100°．
解：∵BE⊥AD，
∴∠BED=90°，
又∵∠ADC=110°，
∴四边形BCDE中，∠BCD+∠CBE=360°-90°-110°=160°，
又∵∠EBC和∠DCB的角平分线相交于点F，
∴∠BCF+∠CBF=×160°=80°，
∴△BCF中，∠F=180°-80°=100°，
故选：D．
练习册系列答案
相关题目
