��Ŀ����
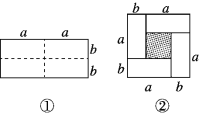
����Ŀ�����ֲ�������ͼ����һ����Ϊ2a����Ϊ2b�ij����Σ���ͼ�е��������ֳ��ĸ���С��ȵij����Σ�Ȼ����ͼ����ʾƴ��һ�������Σ�
������⣺
(1)�۲�ͼ�ڣ��������ֲ�ͬ�ķ�����ʾ��Ӱ���ֵ������_____________��_____________��
(2)��д����������ʽ(a��b)2��(a��b)2��ab֮���һ��������ϵ��___________________________��
����������������(2)�еõ��ĵ�����ϵ������������⣺��֪x��y��8��xy��7����x��y��ֵ��
���𰸡�(1) (a��b)2��(a��b)2��4ab;(2) (a��b)2��4ab��(a��b)2���������� x��y����6
��������
��1����һ�ַ���Ϊ�������������-4��С������������ڶ��ֱ�ʾ����Ϊ����Ӱ���������ε������
��2���ɵõ�����ϵΪ����a+b��2-4ab=��a-b��2�����ã�a+b��2-4ab=��a-b��2����⣮
�⣺������⣺(1) (a��b)2��(a��b)2��4ab.
(2) (a��b)2��4ab��(a��b)2
����������(2)��(x��y)2��(x��y)2��4xy.
��x��y��8��xy��7��
��(x��y)2��64��28��36.
��x��y����6.

��ϰ��ϵ�д�
�����Ŀ