题目内容
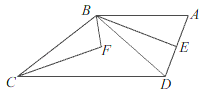
【题目】如图,∠MAN=15°,AB=BC=CD=DE=EF,则∠FEM=________.
![]()
【答案】75°
【解析】
根据已知条件,利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算.
解答:解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠BCD=180°-(∠CBD+∠BDC)=180°-60°=120°,
∴∠ECD=∠CED=180°-∠BCD-∠BCA=180°-120°-15°=45°,
∴∠CDE=180°-(∠ECD+∠CED)=180°-90°=90°,
∴∠EDF=∠EFD=180°-∠CDE-∠BDC=180°-90°-30°=60°,
∴∠MEF=∠EFD+∠A=60°+15°=75°.
故答案为:75°.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目