题目内容
【题目】如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线. 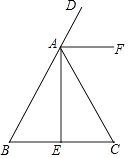
(1)用尺规作图:作∠AEC的平分线EN(保留作图痕迹,不写作法和证明);
(2)设EN与AF交于点M,判断△AEM的形状,并说明理由.
【答案】
(1)解:如图,射线EN即为所求;

(2)解:△ADF是等腰直角三角形.
在△ABC中,
∵AB=AC,AE⊥BC,
∴AE平分∠BAC,
∴∠EAC= ![]() ∠BAC.
∠BAC.
∵AF平分∠CAD,
∴∠CAF= ![]() ∠CAD,
∠CAD,
∴∠EAF= ![]() (∠BAC+∠CAD)=
(∠BAC+∠CAD)= ![]() ×180°=90°,
×180°=90°,
∵∠AEC=90°,EN是∠AEC的平分线,
∴∠AEM=45°,
∴∠AME=45°,
∴AE=AM,即△AEM是等腰直角三角形.
【解析】(1)根据角平分线的作法作∠AEC的平分线EN即可;(2)先根据题意得出AE平分∠BAC,再由AF是△ABC外角∠CAD的平分线可得出∠EAM=90°,根据EN是∠AEC的平分线可得出∠AEM=45°,据此可得出结论.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?