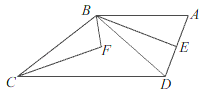
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćA£Ø©3£¬0£©£¬¶ž“ĪŗÆŹży=ax2+bx+ ![]() µÄ¶Ō³ĘÖįĪŖÖ±Ļßx=©1£¬ĘäĶ¼Ļó¹żµćAÓėxÖį½»ÓŚĮķŅ»µćB£¬ÓėyÖį½»ÓŚµćC£®
µÄ¶Ō³ĘÖįĪŖÖ±Ļßx=©1£¬ĘäĶ¼Ļó¹żµćAÓėxÖį½»ÓŚĮķŅ»µćB£¬ÓėyÖį½»ÓŚµćC£®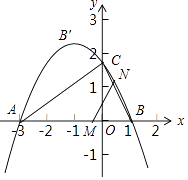
£Ø1£©Ē󶞓ĪŗÆŹżµÄ½āĪöŹ½£¬Š“³ö¶„µć×ų±ź£»
£Ø2£©¶ÆµćM£¬NĶ¬Ź±“ÓBµć³ö·¢£¬¾łŅŌĆæĆė2øöČżĪ»³¤¶ČµÄĖŁ¶Č·Ö±šŃŲ”÷ABCµÄBA£¬BC±ßÉĻŌĖ¶Æ£¬ÉčĘäŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬µ±ĘäÖŠŅ»øöµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬Į¬½įMN£¬½«”÷BMNŃŲMN·ÕŪ£¬ČōµćBĒ”ŗĆĀäŌŚÅ×ĪļĻß»”ÉĻµÄB”䓦£¬ŹŌĒótµÄÖµ¼°µćB”äµÄ×ų±ź£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬QĪŖBNµÄÖŠµć£¬ŹŌĢ½¾æ×ų±źÖįÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆŅŌB£¬Q£¬PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£æČē¹ū“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ŹŌĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ
£Ø1£©
½ā£ŗÓÉĢāŅāµĆ 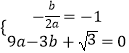 £¬
£¬
½āµĆ 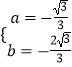 £¬
£¬
¶ž“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=© ![]() x2©
x2© ![]() x+
x+ ![]()
Åä·½µĆy=© ![]() £Øx+1£©2+
£Øx+1£©2+ ![]() £¬
£¬
¶„µć×ų±źĪŖ£Ø©1£¬ ![]() £©£¬
£©£¬
£Ø2£©
½ā£ŗČēĶ¼1
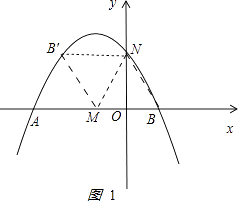 £¬
£¬
ÓÉĢāŅāÖŖOA=3£¬OB=1£¬ON= ![]() £¬
£¬
”ą”ĻCBA=60”ć£¬
ÓÖ”ßBM=BN£¬
”ą”÷MBNŹĒÕżČż½ĒŠĪ£¬
”ąM£Ø1©2t£¬0£©£¬N£Ø1©t£¬ ![]() t£©£®
t£©£®
½«”÷BMNŃŲMN·ÕŪŗ󣬵Ć
B”äN=BN=2t£¬”ĻB”äNM=”ĻBMN=60”ć£¬
”ąB”äN”ĪBM£¬
”ąB”ä£Ø1©3t£¬ ![]() t£©£¬
t£©£¬
ÓÖµćB”äŌŚÅ×ĪļĻßÉĻ£¬
”ą ![]() t=©
t=© ![]() £Ø1©3t£©2©
£Ø1©3t£©2© ![]() £Ø1©3t£©+
£Ø1©3t£©+ ![]() £¬
£¬
»Æ¼ņ£¬µĆ9t2©9t=0£¬½āµĆt=0£Ø²»·ūŗĻĢāŅā£¬Éį£©t=1£¬
t=1Ź±£¬1©3t=©2£¬ ![]() t=
t= ![]() £¬
£¬
”ąB”ä£Ø©2£¬ ![]() £©£»
£©£»
£Ø3£©
½ā£ŗÓÉĢāŅāæɵƔ÷ABCŹĒÖ±½ĒČż½ĒŠĪ£¬ĒŅ”ĻBAC=30”ć£¬”ĻABC=60”ć£®ÓÖQ£Ø ![]() £¬
£¬ ![]() £©£®
£©£®
¢ŁČēĶ¼2
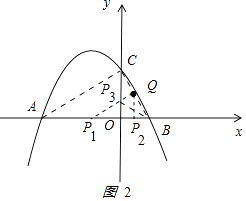 £¬
£¬
ÓÉĢāŅāÖŖOA=3£¬OB=1£¬
PŌŚxÖįÉĻŹ±£¬¹żQ×÷P1Q”ĶBQ½»xÖįÓŚP1µć£¬
”ßP1Q”ĪAC£¬
”ą1BQ”×”÷ABC£¬
![]() =
= ![]() =
= ![]() £¬
£¬
½āµĆP1B=2£¬OP1=1£¬P1£Ø©1£¬0£©£»
¹żQ×÷P2Q”ĶxÖįÓŚP2£¬
”ß”ĻP2BQ=”ĻCBA£¬”ĻQPB=”ĻACB£¬
”ąQBP2”×”÷ABC£¬
![]() =
= ![]() £¬
£¬
½āµĆBP2= ![]() £¬OP2=
£¬OP2= ![]() £¬
£¬
P2£Ø ![]() £¬0£©£»
£¬0£©£»
PŌŚxÖįµÄĘäĖüĪ»ÖĆŹ±£¬”÷PBQ²»æÉÄÜĪŖÖ±½ĒČż½ĒŠĪ£¬²»æÉÄÜÓė”÷ABCĻąĖĘ£»
¢ŚĶ¬Ąķ£¬µ±PŌŚyÖįÉĻŹ±£¬×÷P3Q”ĶBQ½»yÖįÓŚP3£¬
”ß”ĻP3BQ=”ĻBAC=”ĻP3BO=30”ć£¬”ĻP3QB=”ĻACB=90”ć£¬
”ą”÷BP3Q”×”÷ABC£®
”ßtan”ĻP3BO= ![]() =
= ![]() £¬P3O=
£¬P3O= ![]() £¬
£¬
P3£Ø0£¬ ![]() £©£®
£©£®
B×÷P4B”ĶBQ½»yÓŚP4£¬µ« ![]() ”Ł
”Ł ![]() £¬
£¬
”ą”÷QBP4YÓė”÷ABC²»ĻąĖĘ£¬PŌŚyÖįÉĻĘäĖüĪ»ÖĆŹ±£¬”÷PQB²»ĪŖÖ±½ĒČż½ĒŠĪ£¬²»ÄÜÓė”÷ABCĻąĖĘ£»
×ŪÉĻĖłŹö£ŗ×ų±źÖįÉĻ“ęŌŚµćP£¬Ź¹µĆŅŌB£¬Q£¬PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£¬Pµć×ų±źĪŖ£Ø©1£¬0£©£¬£Ø ![]() £¬0£©£¬£Ø0£¬
£¬0£©£¬£Ø0£¬ ![]() £©£®
£©£®
”¾½āĪö”æ£Ø1£©øł¾Ż“ż¶ØĻµŹż·Ø£¬æɵĆŗÆŹż½āĪöŹ½£¬øł¾ŻÅä·½·Ø£¬æɵƶ„µć×ų±ź£»£Ø2£©øł¾ŻµČ±ßČż½ĒŠĪµÄÅŠ¶Ø£¬æɵƔ÷MBNŹĒÕżČż½ĒŠĪ£¬øł¾Ż·ÕŪµÄŠŌÖŹ£¬æɵĆB”äN£¬”ĻB”äNM£¬øł¾ŻĘ½ŠŠĻßµÄÅŠ¶Ø£¬æɵĆB”äµÄׯ×ų±ź£¬øł¾ŻµćµÄ×ų±źĀś×ćŗÆŹż½āĪöŹ½£¬æÉµĆ¹ŲÓŚtµÄ·½³Ģ£¬øł¾Ż½ā·½³Ģ£¬æɵĆt£¬æɵĆB”äµÄ×ų±ź£»£Ø3£©øł¾ŻĻąĖĘČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ£¬æɵƓš°ø£®

”¾ĢāÄæ”æĪŖĮĖ½āijŹŠŹŠĆń”°ĀĢÉ«³öŠŠ”±·½Ź½µÄĒéæö£¬Ä³Š£ŹżŃ§ŠĖȤŠ”×éŅŌĪŹ¾ķµ÷²éµÄŠĪŹ½£¬Ė껜µ÷²éĮĖijŹŠ²æ·Ö³öŠŠŹŠĆńµÄÖ÷ŅŖ³öŠŠ·½Ź½£Ø²ĪÓėĪŹ¾ķµ÷²éµÄŹŠĆń¶¼Ö»“ÓŅŌĻĀĪåøöÖÖĄąÖŠŃ”ŌńŅ»Ąą£©£¬²¢½«µ÷²é½į¹ū»ęÖĘ³ÉČēĻĀ²»ĶźÕūµÄĶ³¼ĘĶ¼£®
ÖÖĄą | A | B | C | D | E |
³öŠŠ·½Ź½ | ¹²Ļķµ„³µ | ²½ŠŠ | ¹«½»³µ | µÄŹæ | Ė½¼Ņ³µ |

øł¾ŻŅŌÉĻŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©²ĪÓė±¾“ĪĪŹ¾ķµ÷²éµÄŹŠĆń¹²ÓŠ ČĖ£¬ĘäÖŠŃ”ŌńBĄąµÄČĖŹżÓŠ ČĖ£»
£Ø2£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬ĒóAĄą¶ŌÓ¦ÉČŠĪŌ²ŠÄ½Ē¦ĮµÄ¶ČŹż£¬²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø3£©øĆŹŠŌ¼ÓŠ12ĶņČĖ³öŠŠ£¬Čō½«A£¬B£¬CÕāČżĄą³öŠŠ·½Ź½¾łŹÓĪŖ”°ĀĢÉ«³öŠŠ”±·½Ź½£¬Ēė¹Ą¼ĘøĆŹŠ”°ĀĢÉ«³öŠŠ”±·½Ź½µÄČĖŹż£®