Question

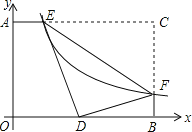
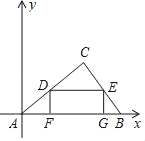
【题目】如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，以点A为原点建立平面直角坐标系，使AB在x轴正半轴上，点D是AC边上的一个动点，DE∥AB交BC于E，DF⊥AB于F，EG⊥AB于G．以下结论：

①△AFD∽△DCE∽△EGB；

②当D为AC的中点时，△AFD≌△DCE；

③点C的坐标为（3.2，2.4）；

④将△ABC沿AC所在的直线翻折到原来的平面，点B的对应点B1的坐标为（1.6，4.8）；

⑤矩形DEGF的最大面积为3．在这些结论中正确的有_____（只填序号）

Answer 1

【答案】①③⑤

【解析】

①正确，根据两角对应相等的两个三角形相似即可判断；

②错误．根据斜边不相等即可判断；

③正确．求出点C坐标即可判断；

④错误．求出点B1即可判断；

⑤正确．首先证明四边形DEGF是矩形，推出DF=EG，DE=FG，设DF=EG=x，构建二次函数，利用二次函数的性质即可判断.

如图，作CH⊥AB于H．

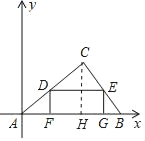
∵DF⊥AB于F，EG⊥AB于G，

∴∠AFD＝∠DCE＝∠EGB＝90°，

∵DE∥AB，

∴∠CDE＝∠DAF，∠CED＝∠EBG，

∴△AFD∽△DCE∽△EGB；故①正确；

当AD＝CD时，∵DE＞CD，

∴DE＞AD，

∴△AFD与△DCE不全等，故②错误，

在Rt△ACB中，∵AC＝4，BC＝3，

∴AB＝5，CH＝4，

∴AH＝＝3.2，

∴C（3.2，2.4），故③正确，

将△ABC沿AC所在的直线翻折到原来的平面，点B的对应点B1，设B1为（m，n），

则有＝3.2，m＝1.4，

＝2.4，n＝4.8，

∴B1（1.4，4.8），故④错误；

∵DF⊥AB于F，EG⊥AB于G，

∴DF∥EG，

∵DE∥AB，

∴四边形DEGF是平行四边形，

∵∠DFG＝90°，

∴四边形DEGF是矩形，

∴DF＝EG，DE＝FG，设DF＝EG＝x，则AF=x，BG＝x，

∴DE＝FG＝5﹣x﹣x＝5﹣x，

∵S矩形DEGF＝x（5﹣x）＝﹣x2+5x，

∵﹣＜0，

∴S的最大值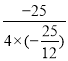＝＝3，故⑤正确，

综上所述，正确的有：①③⑤，

故答案为①③⑤．