题目内容
【题目】郑州市创建国家生态园林城市实施方案已经出台,到2019年5月底,市区主城区要达到或超过《国家生态园林城市标准》各项指标要求.郑州市林荫路推广率要超过85%,在推进此活动中,郑州市某小区决定购买A、B两种乔木树,经过调查,获取信息如下:如果购买A种树木40棵,B种树木60棵,需付款11400元;如果购买A种树木50棵,B种树木50棵,需付款10500元.
树种 | 购买数量低于50棵 | 购买数量不低于50棵 |
A | 原价销售 | 以八折销售 |
B | 原价销售 | 以九折销售 |
(1)A种树木与B种树木的单价各多少元?
(2)经过测算,需要购置A、B两种树木共100棵,其中B种树木的数量不多于A种树木的三分之一,如何购买付款最少?最少费用是多少元?请说明理由.
【答案】(1)A种树每棵150元,B种树每棵100元;(2)当购买A种树木75棵,B种树木25棵时,所需费用最少,最少为11500元.
【解析】
(1)设A种树每棵x元,B种树每棵y元,根据“购买A种树木40棵,B种树木60棵,需付款11400元;如果购买A种树木50棵,B种树木50棵,需付款10500元”列出方程组并解答;
(2)设购买A种树木为a棵,则购买B种树木为(100﹣a)棵,根据“B种树木的数量不多于A种树木的三分之一”列出不等式并求得a的取值范围,再根据一次函数的性质解答即可.
解:(1)设A种树每棵x元,B种树每棵y元,
依题意得:![]() ,解得
,解得![]() ,
,
即A种树每棵150元,B种树每棵100元;
(2)设购买A种树木为a棵,则购买B种树木为(100﹣a)棵,
则(100﹣a)![]() ,
,
解得a≥75.
设实际付款总金额是y元,则
y=0.8×150a+100(100﹣a),即y=20a+10000.
∵k=20>0,y随a的增大而增大,
∴当a=75时,y最小.
即当a=75时,y最小值=20×75+10000=11500(元).
答:当购买A种树木75棵,B种树木25棵时,所需费用最少,最少为11500元.

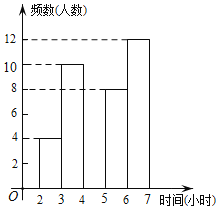
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?