题目内容
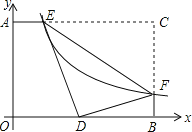
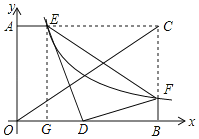
【题目】如图,反比例函数![]() 的图象与矩形AOBC的边AC,BC分别相交于点E,F,点C的坐标为(4,3)将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
的图象与矩形AOBC的边AC,BC分别相交于点E,F,点C的坐标为(4,3)将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
A. ![]() B. 6C. 3D.
B. 6C. 3D. ![]()
【答案】D
【解析】
过点E作EG⊥OB于点G,根据折叠的性质得∠EDF=∠ACB=90°,EC=ED,CF=DF,易证△GED∽△BDF;再根据EG:DB=ED:DF=4:3,即可求出BD,然后在Rt△DBF中利用勾股定理得到关于k的方程,解方程求出k的值即可.
如图,过点E作EG⊥OB于点G,
∵将△CEF沿EF对折后,C点恰好落在OB上的D点处,
∴∠EDF=∠ACB=90°,EC=ED,CF=DF,
∴∠GDE+∠FDB=90°,而EG⊥OB,
∴∠GDE+∠GED=90°,
∴∠GED=∠FDB,
∴△GED∽△BDF;
又∵EC=AC﹣AE=![]() ,CF=BC﹣BF=3﹣
,CF=BC﹣BF=3﹣![]() ,
,
∴ED=![]() ,DF=3﹣
,DF=3﹣![]() ,
,
∴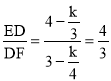
∴EG:DB=ED:DF=4:3,而EG=3,
∴DB=![]() ,
,
在Rt△DBF中,DF2=DB2+BF2,
即![]()
解得k=![]() ,
,
故选:D.

练习册系列答案
相关题目