题目内容
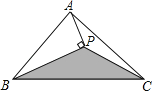
【题目】如图，△ABC的面积为10cm2，BP平分∠ABC，AP⊥BP，垂足为P，连接CP，若三角形内有一点M，则点M落在△BPC内（包括边界）的概率为_____．
【答案】
【解析】
根据已知条件证得△ABP≌△EBP，根据全等三角形的性质得到AP＝PE，得出S△ABP＝S△EBP，S△ACP＝S△ECP，推出S△PBC＝S△ABC，根据概率公式可得的答案．
解：延长AP交BC于E，
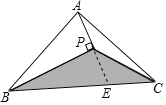
∵BP平分∠ABC，
∴∠ABP＝∠EBP，
∵AP⊥BP，
∴∠APB＝∠EPB＝90°，
在△ABP和△EBP中，
，
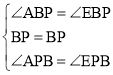∴△ABP≌△EBP（ASA），
∴AP＝PE，
∴S△ABP＝S△EBP，S△ACP＝S△ECP，
∴S△PBC＝S△ABC＝×10cm2＝5cm2，
则点M落在△BPC内（包括边界）的概率为
.
故答案为：.
练习册系列答案
相关题目
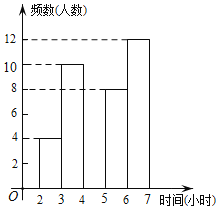
【题目】某中学为了了解学生每周在校体育锻炼时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表，请根据图表信息解答下列问题：
时间（小时） | 频数（人数） | 频率 |
2≤t＜3 | 4 | 0.1 |
3≤t＜4 | 10 | 0.25 |
4≤t＜5 | a | 0.15 |
5≤t＜6 | 8 | b |
6≤t＜7 | 12 | 0.3 |
合计 | 40 | 1 |
（1）表中的a= ，b= ；
（2）请将频数分布直方图补全；
（3）若该校共有1200名学生，试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名？
