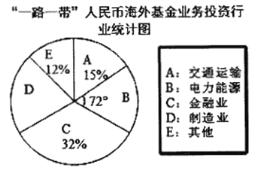
题目内容
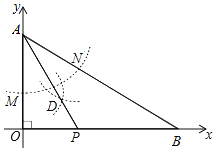
【题目】如图,点A(0,2),在x轴上取一点B,连接AB,以A为圆心,任意长为半径画弧,分别交OA、AB于点M、N,再以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
A. (1,0)B. (![]() ,0)C. (
,0)C. (![]()
![]() ,0)D. (2
,0)D. (2![]() ,0)
,0)
【答案】C
【解析】
根据点D的画法可得出AD平分∠OAB,由角平分线的性质结合相似三角形的性质可得出∠OBA=![]() ∠OAB,利用二角互补即可求出∠OBA=∠OAP=30°,通过解含30度角的直角三角形即可得出点P的坐标.
∠OAB,利用二角互补即可求出∠OBA=∠OAP=30°,通过解含30度角的直角三角形即可得出点P的坐标.
解:由点D的画法可知AD平分∠OAB.
∵△OPA∽△OAB,
∴∠OAP=∠OBA=![]() ∠OAB.
∠OAB.
∵∠OAB+∠OBA=∠OAB+![]() ∠OAB=90°,
∠OAB=90°,
∴∠OAB=60°,∠OAP=30°,
∴AP=2OP.
在Rt△OAP中,∠AOP=90°,OA=2,
![]() ,
,
∴OP=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
故选:C.

练习册系列答案
相关题目