题目内容
【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.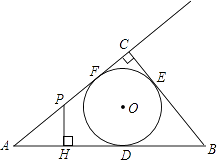
(1)直接写出线段AC、AD及⊙O半径的长;
(2)设PH=x,PC=y,求y关于x的函数关系式;
(3)当PH与⊙O相切时,求相应的y值.
【答案】
(1)
解:AC=4,AD=3,⊙O的半径长为1.
(如图1,连接AO、DO.

设⊙O的半径为r.
在Rt△ABC中,由勾股定理得AC= ![]() =4,
=4,
则⊙O的半径r= ![]() (AC+BC﹣AB)=
(AC+BC﹣AB)= ![]() ×(4+3﹣5)=1;
×(4+3﹣5)=1;
∵CE、CF是⊙O的切线,∠ACB=90°,
∴∠CFO=∠FCE=∠CEO=90°,OF=OE,
∴四边形CEOF是正方形,
∴CF=OF=1;
又∵AD、AF是⊙O的切线,
∴AF=AD;
∴AF=AC﹣CF=AC﹣OF=4﹣1=3,即AD=3);
(2)
解:①如图1,若点P在线段AC上时.
在Rt△ABC中,AB=5,AC=4,BC=3,
∵∠C=90°,PH⊥AB,
∴∠C=∠PHA=90°,
∵∠A=∠A,
∴△AHP∽△ACB,
∴ ![]() ,
,
即 ![]() ,
,
∴y=﹣ ![]() x+4,即y与x的函数关系式是y=﹣
x+4,即y与x的函数关系式是y=﹣ ![]() x+4(0≤x≤2.4);
x+4(0≤x≤2.4);
②同理,当点P在线段AC的延长线上时,△AHP∽△ACB,
则 ![]() ,
,
即 ![]() ,
,
∴y= ![]() x﹣4,即y与x的函数关系式是y=
x﹣4,即y与x的函数关系式是y= ![]() x﹣4(x>2.4);
x﹣4(x>2.4);
(3)
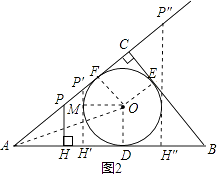
解:①当点P在线段AC上时,如图2,P′H′与⊙O相切于点M.
∵∠OMH′=∠MH′D=∠H′DO=90°,OM=OD,
∴四边形OMH′D是正方形,
∴MH′=OM=1;
由(1)知,四边形CFOE是正方形,
CF=OF=1,
∴P′H′=P′M+MH′=P′F+FC=P′C,即x=y;
又由(2)知,y=﹣ ![]() x+4,
x+4,
∴y=﹣ ![]() y+4,
y+4,
解得y= ![]() .
.
②当点P在AC的延长线上时,如图,P″H″与⊙O相切.此时y=1.
【解析】(1)由勾股定理求AC的长度;设⊙O的半径为r,则r= ![]() (AC+BC﹣AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;(2)分类讨论:①当点P在线段AC上时,通过相似三角形△AHP∽△ACB的对应边成比例知,
(AC+BC﹣AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;(2)分类讨论:①当点P在线段AC上时,通过相似三角形△AHP∽△ACB的对应边成比例知, ![]() ,将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式;②当点P在线段AC的延长线上时,同理,利用相似三角形的性质求得y关于x的函数关系式;(3)根据圆的切线定理证得四边形OMH′D、四边形CFOE为正方形;然后利用正方形的性质、圆的切线定理推知P′H′=P′M+MH′=P′F+FC=P′C,即x=y;最后将其代入(2)中的函数关系式即可求得y值.
,将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式;②当点P在线段AC的延长线上时,同理,利用相似三角形的性质求得y关于x的函数关系式;(3)根据圆的切线定理证得四边形OMH′D、四边形CFOE为正方形;然后利用正方形的性质、圆的切线定理推知P′H′=P′M+MH′=P′F+FC=P′C,即x=y;最后将其代入(2)中的函数关系式即可求得y值.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为________元.