题目内容
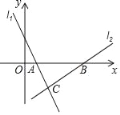
【题目】如图,直线y= ![]() x与双曲线y=
x与双曲线y= ![]() 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).
(1)求A、B两点的坐标及双曲线的解析式;
(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.
【答案】
(1)
解:∵BC⊥x,C(﹣4,0),
∴B的横坐标是﹣4,代入y= ![]() x得:y=﹣1,
x得:y=﹣1,
∴B的坐标是(﹣4,﹣1),
∵把B的坐标代入y= ![]() 得:k=4,
得:k=4,
∴y= ![]() ,
,
∵解方程组 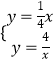 得:
得: ![]() ,
, ![]() ,
,
∴A的坐标是(4,1),
即A(4,1),B(﹣4,﹣1),反比例函数的解析式是y= ![]() .
.
(2)
解:设OE=x,OD=y,
由三角形的面积公式得: ![]() xy﹣
xy﹣ ![]() x1=10,
x1=10, ![]() x4=10,
x4=10,
解得:x=5,y=5,
即OD=5,
∵OC=|﹣4|=4,
∴CD的值是4+5=9.
【解析】(1)求出B的横坐标,代入y= ![]() x求出y,即可得出B的坐标,把B的坐标代入y=
x求出y,即可得出B的坐标,把B的坐标代入y= ![]() 求出y=
求出y= ![]() ,解方程组
,解方程组 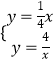 即可得出A的坐标;(2)设OE=x,OD=y,由三角形的面积公式得出
即可得出A的坐标;(2)设OE=x,OD=y,由三角形的面积公式得出 ![]() xy﹣
xy﹣ ![]() y1=10,
y1=10, ![]() x4=10,求出x、y,即可得出OD=5,求出OC,相加即可.
x4=10,求出x、y,即可得出OD=5,求出OC,相加即可.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目