题目内容
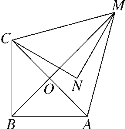
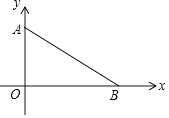
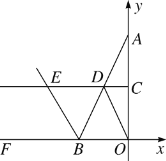
【题目】如图，在平面直角坐标系中，已知点A(0，6)，B(b，0)，且b＜0，C，D分别是OA，AB的中点，△AOB的外角∠DBF的平分线BE与CD的延长线交于点E.
(1)求证：∠DAO＝∠DOA；
(2)①若b＝－8，求CE的长；
②若CE＝
＋1，则b＝________；
(3)是否存在这样的b值，使得四边形OBED为平行四边形？若存在，请求出此时四边形OBED对角线的交点坐标；若不存在，请说明理由．
【答案】(1)见解析；(2) ①9；②－2；(3)见解析.
【解析】(1)由C，D分别为AO，AB的中点，得到CD∥OB．又由OB⊥AO，得到CD垂直平分AO，由垂直平分线的性质即可得到结论．
(2)①由三角形中位线定理得到CD的长，由角平分线的定义和平行线的性质得到∠DEB＝∠DBE，从而得到ED＝BD＝5，即可得到结论．
②由①得：EC=ED+DC=
AB+BO，列方程求解即可得到结论．
(3)由四边形OBED是平行四边形，得OB＝ED．由ED＝BD＝AB，得到AB＝－2b，于是有(－b)2＋62＝(－2b)2，解方程得到b的值，进而得到AB的长．设平行四边形OBED的对角线交点为M，作MH⊥OB于点H，则BM＝BD＝
AB．由OD＝DB＝OB，得到∠DBO＝60°，∠BMH＝30°，从而可得到BH，MH， OH，即可得到结论．
(1)∵C，D分别为AO，AB的中点，∴CD∥OB．
又∵OB⊥AO，∴CD⊥AC，∴CD垂直平分AO，∴AD＝OD，∴∠DAO＝∠DOA．
(2)①∵b＝－8，∴OB＝8，∴CD＝OB＝4．易得∠DEB＝∠DBE，∴ED＝BD＝AB＝
＝5，∴CE＝CD＋ED＝4＋5＝9．
②由①得：EC=ED+DC=AB+BO，∴
，解得：b=－2．故答案为：－2．
(3)存在．理由如下：
如图，∵四边形OBED是平行四边形，∴OB＝ED．
∵ED＝BD＝AB，∴OB＝AB．
∵OB＝－b，∴AB＝－2b，∴(－b)2＋62＝(－2b)2，解得：b＝
，∴AB＝
．设平行四边形OBED的对角线交点为M，作MH⊥OB于点H，则BM＝BD＝AB＝×＝
．
∵OD＝AD，∴OD＝DB＝OB，∴∠DBO＝60°，∴∠BMH＝30°，∴BH＝
，MH＝
，∴OH＝
=
，∴M（
，）．
