题目内容
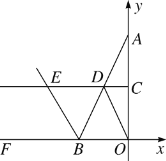
【题目】如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上 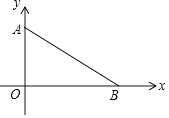
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若函数y= ![]() 的图象经过点M,且sin∠OAB=
的图象经过点M,且sin∠OAB= ![]() ,求k的值.
,求k的值.
【答案】
(1)解:点M为所求作;
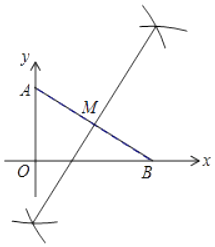
(2)解:∵sin∠OAB= ![]() ,
,
∴设OB=4x,AB=5x,
∴由勾股定理可知:32+(4x)2=(5x)2,
∴x=1,
∴OB=4,
由作图可知M为AB的中点,
∴M(2, ![]() ),
),
将M的坐标代入y= ![]() 中,
中,
∴k=2× ![]() =3,
=3,
【解析】(1)作AB的垂直平分线交AB于点M,此时点M到点A,点B和原点O这三点的距离相等.(2)利用勾股定理可求出点B的坐标,由(1)可知:M是AB的中点,从而可求出M的坐标.
【考点精析】认真审题,首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目