题目内容
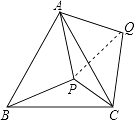
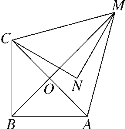
【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
【答案】(1)15°;(2)证明见解析;(3)![]()
【解析】(1)由旋转可得∠ACM=60°,再根据等腰直角三角形MNC中,∠MCN=45°,运用角的和差关系进行计算即可得到∠NCO的度数;
(2)根据有一个角是60°的等腰三角形是等边三角形进行证明即可;
(3)根据△MNC是等腰直角三角形,△ACM是等边三角形,判定△ACN≌△AMN,再根据Rt△ACD中,AD=![]() CD=
CD=![]() ,等腰Rt△MNC中,DN=
,等腰Rt△MNC中,DN=![]() CM=1,即可得到AN=AD﹣ND=
CM=1,即可得到AN=AD﹣ND=![]() ﹣1.
﹣1.
(1)由旋转可得∠ACM=60°.
又∵等腰直角三角形MNC中,∠MCN=45°,∴∠NCO=60°﹣45°=15°;
故答案为:15°;
(2)∵∠ACM=60°,CM=CA,∴△CAM为等边三角形;
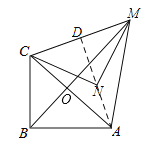
(3)连接AN并延长,交CM于D.
∵△MNC是等腰直角三角形,△ACM是等边三角形,∴NC=NM=![]() ,CM=2,AC=AM=2.在△ACN和△AMN中,∵
,CM=2,AC=AM=2.在△ACN和△AMN中,∵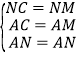 ,∴△ACN≌△AMN(SSS),∴∠CAN=∠MAN,∴AD⊥CM,CD=
,∴△ACN≌△AMN(SSS),∴∠CAN=∠MAN,∴AD⊥CM,CD=![]() CM=1,∴Rt△ACD中,AD=
CM=1,∴Rt△ACD中,AD=![]() CD=
CD=![]() ,等腰Rt△MNC中,DN=
,等腰Rt△MNC中,DN=![]() CM=1,∴AN=AD﹣ND=
CM=1,∴AN=AD﹣ND=![]() ﹣1.
﹣1.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】某校九年级(1)班全体学生上周末进行体育测试的成绩(满分70分)统计如表:
成绩(分) | 45 | 50 | 55 | 60 | 65 | 68 | 70 |
人数(人) | 2 | 6 | 10 | 7 | 6 | 5 | 4 |
根据表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学
B. 该班学生这次测试成绩的众数是55分
C. 该班学生这次测试成绩的中位数是60分
D. 该班学生这次测试成绩的平均数是59分