题目内容
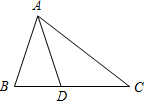
已知：直角三角形的一个锐角等于另一个锐角的2倍，这个角的平分线把对边分成两条线段，求证：其中一条是另一条的2倍．
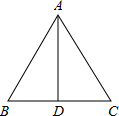
已知：在△ABC中，∠C=90°，∠A=2∠B，AD平分∠CAB交BC于D，
求证：BD=2DC．
证明：在Rt△ABC中，
∵∠C=90°，∠CAB=2∠B，
∴∠CAB=60°，∠B=30°．
∵AD平分∠CAB，
∴∠CAD=∠DAB=30°．
在△ABD中
∵∠CAD=∠DAB=30°，
∴AD=BD．
在△ADC中，
∵∠CAD=30°，
∴AD=2CD．
∴BD=2CD．
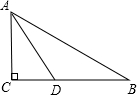
求证：BD=2DC．
证明：在Rt△ABC中，
∵∠C=90°，∠CAB=2∠B，
∴∠CAB=60°，∠B=30°．
∵AD平分∠CAB，
∴∠CAD=∠DAB=30°．
在△ABD中
∵∠CAD=∠DAB=30°，
∴AD=BD．
在△ADC中，
∵∠CAD=30°，
∴AD=2CD．
∴BD=2CD．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
相关题目
