Question

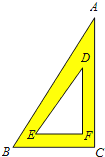
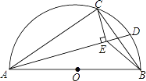
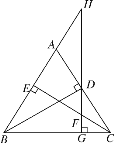
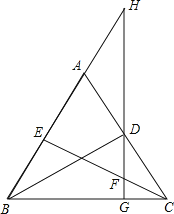
【题目】如图，BD，CE分别是△ABC的两边上的高，过D作DG⊥BC于G，分别交CE及BA的延长线于F，H，求证：

(1)DG2＝BG·CG；

(2)BG·CG＝GF·GH.

Answer 1

【答案】

【1】 证明：∵BD⊥AC，DG⊥BC，

∴

∠DBC+∠DCG=∠GDC+∠DCG，

∴∠GDC=∠DBC，

∴

∴BG:DG=DG:CG，

即

【2】 同(1)中的方法,同理可证：△BGH∽△FGC，

∴BG:GF=GH:CG，

∴BGCG=GFGH.

【解析】

（1）根据题意结合图形，证明列出比例式，化为等积式即可解决问题．
（2）方法同（1）中的解法，证明△BGH∽△FGC，列出比例式，化为等积式即可解决问题．

证明：(1)∵BD⊥AC，DG⊥BC，

∴

∠DBC+∠DCG=∠GDC+∠DCG，

∴∠GDC=∠DBC，

∴

∴BG:DG=DG:CG，

即

(2)同(1)中的方法,同理可证：△BGH∽△FGC，

∴BG:GF=GH:CG，

∴BGCG=GFGH.