Question

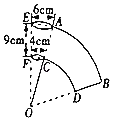
【题目】市政规划出一块矩形土地用于某项目开发，其中，设计分区如图所示，为矩形内一点，作于点交于点，过点作交于点，其中丙区域用于主建筑区，其余各区域均用于不同种类绿化．

若点是的中点，求的长；

要求绿化占地面积不小于，规定乙区域面积为

①若将甲区域设计成正方形形状，能否达到设计绿化要求?请说明理由；

②若主建筑丙区域不低于乙区域面积的，则的最大值为 （请直接写出答案）

Answer 1

【答案】（1）90m；（2）①能达到设计绿化要求，理由见解析，②40

【解析】

（1）首先理由矩形性质得出AD=BC=180m，AB∥CD，AD∥BC，进一步证明出四边形AFEG与四边形DGEH为矩形，四边形BIHE为平行四边形，由此得出AG=EF，DG=EH，EH=BI，据此进一步求解即可；

（2）①设正方形AFEG边长为m，根据题意列出方程，然后进一步求解再加以分析即可；②设AF=m，则EH=m，然后结合题意列出不等式，最后再加以求解即可.

（1）∵四边形ABCD为矩形，

∴AD=BC=180m，AB∥CD，AD∥BC，

∵EG⊥AD，EH∥BC，HI∥BE，

∴四边形AFEG与四边形DGEH为矩形，四边形BIHE为平行四边形，

∴AG=EF，DG=EH，EH=BI，

∵点G为AD中点，

∴DG=AD=90m，

∴BI=EH=DG=90m；

（2）①能达到设计绿化要求，理由如下：

设正方形AFEG边长为m，

由题意得：，

解得：，

当时，EH=m，

则EF=180150=30m，符合要求，

∴若将甲区域设计成正方形形状，能达到设计绿化要求；

②设AF=m，则EH=m，

由题意得：，

解得：，

即AF的最大值为40m，

故答案为：40.