题目内容
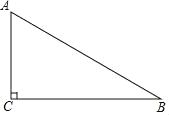
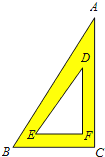
【题目】一块含30°角的直角三角板（如图），它的斜边AB=8cm，里面空心△DEF的各边与△ABC的对应边平行，且各对应边的距离都是1cm，那么△DEF的周长是（ ）
A、5cm B、6cm C、（6-
）cm D、（3+）cm
【答案】B．
【解析】
试题根据相似三角形的周长的比等于相似比可求△DEF的周长，求出EF的长是解决本题的关键．
试题解析：∵斜边AB=8cm，∠A=30°，
∴BC=4cm，AC=4
cm，周长是12+4cm，
连接BE，过E作EM⊥BC于M，
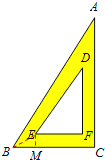
则∠EBC=30°，EM=1cm，
∴BM=cm．
则EF=4-1-=3-cm．
∴△ABC∽△DEF，
相似比是
，
相似三角形周长的比等于相似比，
因而
，
解得△DEF的周长是6cm．
故选B．
练习册系列答案
相关题目
