ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩάύ±»Β»―ϋ»ΐΫ«–ΈΒΡΕ®“εΘ§Έ“Ο«Ε®“εΘΚ”–“ΜΉιΝΎ±ΏœύΒ»ΒΡΆΙΥΡ±Ώ–ΈΫ–ΉωΓΑΒ»ΝΎ±ΏΥΡ±Ώ–ΈΓ±Θ°
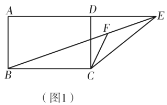
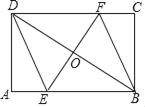
Θ®1Θ©»γΆΦ 1Θ§‘ΎΥΡ±Ώ–Έ ABCD ÷–Θ§ΧμΦ”“ΜΗωΧθΦΰ ΙΒΟΥΡ±Ώ–Έ ABCD «ΓΑΒ»ΝΎ±ΏΥΡ±Ώ–ΈΓ±Θ°«κ–¥≥ωΡψΧμΦ”ΒΡ“ΜΗωΧθΦΰΘ°
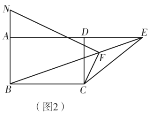
Θ®2Θ©–ΓΚλ≤¬œκΘΚΕ‘Ϋ«œΏΜΞœύΤΫΖ÷ΒΡΓΑΒ»ΝΎ±ΏΥΡ±Ώ–ΈΓ± «Νβ–ΈΘ°ΥΐΒΡ≤¬œκ’ΐ»Ζ¬πΘΩ«κΥΒΟςάμ”…Θ°
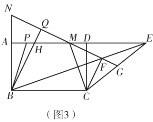
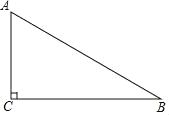
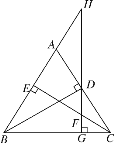
Θ®3Θ©»γΆΦ 2Θ§–ΓΚλΉςΝΥ“ΜΗωRtΓςABCΘ§Τδ÷–ΓœABCΘΫ90ΓψΘ§ABΘΫ2Θ§BCΘΫ1Θ§≤ΔΫΪ RtΓςABC ―ΊΓœABC ΒΡΤΫΖ÷œΏ BBΓδΖΫœρΤΫ“ΤΒΟΒΫΓςAΓδBΓδCΓδΘ§Ν§Ϋα AAΓδΘ§ BCΓδΘ°–ΓΚλ“Σ ΙΒΟΤΫ“ΤΚσΒΡΥΡ±Ώ–Έ ABCΓδAΓδ «ΓΑΒ»ΝΎ±ΏΥΡ±Ώ–ΈΓ±Θ§”ΠΤΫ“ΤΕύ…ΌΨύάκΘ®Φ¥œΏΕΈ BΓδB ΒΡ≥ΛΘ©ΘΩ
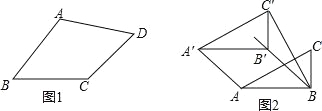
ΓΨ¥πΑΗΓΩΘ®1Θ©ABΘΫBC Μρ BCΘΫCD Μρ CDΘΫAD Μρ ADΘΫABΘΜΘ®2Θ©ΫβΘΚ–ΓΚλΒΡΫα¬έ’ΐ»ΖΘ§άμ”…œξΦϊΫβΈωΘΜΘ®3Θ©ΤΫ“Τ 2 Μρ![]() Μρ
Μρ![]() Μρ
Μρ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”…ΓΑΒ»ΝΎ±ΏΥΡ±Ώ–ΈΓ±ΒΡΕ®“ε“ΉΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©ΔΌœ»άϊ”ΟΤΫ––ΥΡ±Ώ–ΈΒΡ≈–Ε®Ε®άμΒΟΤΫ––ΥΡ±Ώ–ΈΘ§‘Όάϊ”ΟΓΑΒ»ΝΎ±ΏΥΡ±Ώ–ΈΓ±Ε®“εΒΟΝΎ±ΏœύΒ»Θ§ΒΟ≥ωΫα¬έΘΜ
ΔΎ”…ΤΫ“ΤΒΡ–‘÷ “ΉΒΟBBΓδ=AAΓδΘ§AΓδBΓδΓΈABΘ§AΓδBΓδ=AB=2Θ§BΓδCΓδ=BC=1Θ§AΓδCΓδ=AC=5Θ§‘Όάϊ”ΟΓΑΒ»ΝΎ±ΏΥΡ±Ώ–ΈΓ±Ε®“εΖ÷άύΧ÷¬έΘ§”…Ι¥Ι…Ε®άμΒΟ≥ωΫα¬έΘΜ
Θ®3Θ©”…–ΐΉΣΒΡ–‘÷ Ω…ΒΟΓςABFΓ’ΓςADCΘ§”…»ΪΒ»–‘÷ ΒΟΓœABF=ΓœADCΘ§ΓœBAF=ΓœDACΘ§AF=ACΘ§FB=CDΘ§άϊ”ΟœύΥΤ»ΐΫ«–Έ≈–Ε®ΒΟΓςACFΓΉΓςABDΘ§”…œύΥΤΒΡ–‘÷ ΚΆΥΡ±Ώ–ΈΡΎΫ«ΚΆΒΟΓœCBF=90ΓψΘ§άϊ”ΟΙ¥Ι…Ε®άμΘ§Β»ΝΩ¥ζΜΜΒΟ≥ωΫα¬έΘ°
Θ®1Θ©ΫβΘΚABΘΫBC Μρ BCΘΫCD Μρ CDΘΫAD Μρ ADΘΫAB
Θ®2Θ©ΫβΘΚ–ΓΚλΒΡΫα¬έ’ΐ»ΖΘ°
άμ”…»γœ¬ΘΚΓΏΥΡ±Ώ–ΈΒΡΕ‘Ϋ«œΏΜΞœύΤΫΖ÷Θ§
Γύ’βΗωΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓΏΥΡ±Ώ–Έ «ΓΑΒ»ΝΎ±ΏΥΡ±Ώ–ΈΓ±Θ§
Γύ’βΗωΥΡ±Ώ–Έ”–“ΜΉιΝΎ±ΏœύΒ»Θ§
Γύ’βΗωΓΑΒ»ΝΎ±ΏΥΡ±Ώ–ΈΓ± «Νβ–ΈΘ§
Θ®3Θ©ΫβΘΚ”…ΓœABCΘΫ90ΓψΘ§ABΘΫ2Θ§BCΘΫ1Θ§ΒΟΘΚACΘΫ ![]() Θ§
Θ§
ΓΏΫΪ RtΓςABC ΤΫ“ΤΒΟΒΫ RtΓςAΓδBΓδCΓδΘ§
ΓύBAΓδΘΫAAΓδΘ§AΓδBΓδΓΈABΘ§AΓδBΓδΘΫABΘΫ2Θ§BΓδCΓδΘΫBCΘΫ1Θ§AΓδCΓδΘΫACΘΫ![]() Θ§
Θ§
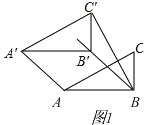
ΔΌ»γΆΦ 1Θ§Β± AAΓδΘΫAB ±Θ§BBΓδΘΫAAΓδΘΫABΘΫ2Θ§

ΔΎ»γΆΦ 2Θ§Β± AAΓδΘΫAΓδCΓδ ±Θ§BBΓδΘΫAAΓδΘΫACΓδΘΫ![]() Θ§
Θ§
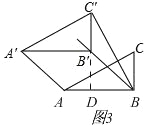
ΔέΒ± ACΓδΘΫBCΓδΘΫ![]() ±Θ§»γΆΦ 3Θ§―”≥Λ CΓδBΓδΫΜ AB ”ΎΒψ DΘ§‘ρ CΓδBΓδΓΆAB
±Θ§»γΆΦ 3Θ§―”≥Λ CΓδBΓδΫΜ AB ”ΎΒψ DΘ§‘ρ CΓδBΓδΓΆAB
ΓΏBBΓδΤΫΖ÷ΓœABCΘ§
ΓύΓœABBΓδΘΫ ![]() ΓœABCΘΫ45Γψ
ΓœABCΘΫ45Γψ
ΓύΓœBBΓδDΘΫΓœABBΓδΘΫ45ΓψΘ§
ΓύBΓδDΘΫBDΘ§
…η BΓδDΘΫBDΘΫxΘ§‘ρ CΓδDΘΫx+1Θ§BBΓδΘΫ![]() x
x
ΓΏΗυΨί‘Ύ RtΓςBCΓδD ÷–Θ§BCΓδ2ΘΫCΓδD2+BD2 Φ¥ x2+Θ®x+1Θ©2ΘΫ5
ΫβΒΟΘΚxΘΫ1 Μρ xΘΫ©¹2Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©
ΓύBBΓδΘΫ![]()
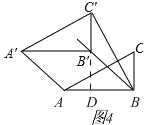
ΔήΒ±BCΓδΘΫABΘΫ2 ±Θ§»γΆΦ4Θ§”κΘ®IIIΘ©ΖΫΖ®Ά§άμΩ…ΒΟΘΚ![]() Θ®…α»ΞΘ©
Θ®…α»ΞΘ©
Γύ ![]() .
.
Ι ”ΠΤΫ“Τ 2 Μρ![]() Μρ
Μρ![]() Μρ
Μρ![]() Θ°
Θ°

 ≥ε¥Χ100Ζ÷ΒΞ‘Σ”≈Μ·ΝΖΩΦΨμœΒΝ–¥πΑΗ
≥ε¥Χ100Ζ÷ΒΞ‘Σ”≈Μ·ΝΖΩΦΨμœΒΝ–¥πΑΗ