题目内容
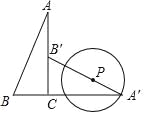
【题目】⊙O 的直径 AB 长为 10,弦 MN⊥AB,将⊙O 沿 MN 翻折,翻折后点 B 的对应点为点 B′,若 AB′=2,MB′的长为( )
A. 2 ![]() B. 2
B. 2![]() 或 2
或 2![]() C. 2
C. 2![]() D. 2
D. 2 ![]() 或 2
或 2![]()
【答案】B
【解析】
分点 B'在线段 AB 上,点 B'在 BA 延长线上两种情况讨论,根据勾股定理可求 MB'的长度.
①如图:当点B'在线段AB上,连接OM,
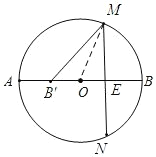
∵AB=10,AB'=2,
∴AO=BO=5=OM,BB'=8,
∴B'O=3,
由折叠可得BE=B'E=4,
∵B'O=3,
∴OE=1,
在Rt△OME中,ME2=OM2﹣OE2=25﹣1=24,
在 Rt△B'ME 中,B'M=![]() ,
,
②若点B'在BA的延长线上,连接OM,
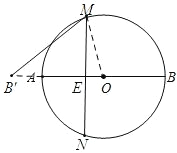
∵AB'=2,AB=10,
∴B'B=12,AO=BO=OM=5,
有折叠可得E=6,
∴OE=BE﹣BO=1,
在Rt△MEO,ME2=MO2﹣OE2=25﹣1=24,
在 Rt△B'ME 中,B'M=![]() ,
,
上所述 B'M=2![]() 或 2
或 2![]() ,
,
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目