题目内容
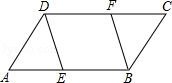
探究:已知平行四边形ABCD的面积为100,M是AB所在直线上的一点
(1)如图1:当点M与B重合时,S△DCM =________;

(2)如图2:当点M与B与A均不重合时,S△DCM =________
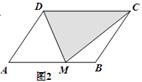
(3)如图3:当点M在AB(或BA)的延长线上时,S△DCM =________

推广:平行四边形ABCD的面积为a,E、F为两边DC、BC延长线上两点,连接DF、AF、AE、BE.求出图4中阴影部分的面积,并简要说明理由

应用:如图5是某广场的一平行四边形绿地ABCD,PQ、MN分别平行DC、AD,PQ、MN交于O点,其中S四边形AM OP=300m2,S四边形MBQO=400m2,S四边形NCQO=700m2.现进行绿地改造,在绿地内部做一个三角形区域MQD,连接DM、QD、QM,(图中阴影部分)种植不同的花草,求三角形DMQ区域的面积.

(1)如图1:当点M与B重合时,S△DCM =________;

(2)如图2:当点M与B与A均不重合时,S△DCM =________

(3)如图3:当点M在AB(或BA)的延长线上时,S△DCM =________

推广:平行四边形ABCD的面积为a,E、F为两边DC、BC延长线上两点,连接DF、AF、AE、BE.求出图4中阴影部分的面积,并简要说明理由

应用:如图5是某广场的一平行四边形绿地ABCD,PQ、MN分别平行DC、AD,PQ、MN交于O点,其中S四边形AM OP=300m2,S四边形MBQO=400m2,S四边形NCQO=700m2.现进行绿地改造,在绿地内部做一个三角形区域MQD,连接DM、QD、QM,(图中阴影部分)种植不同的花草,求三角形DMQ区域的面积.

(1)50;(2)50;(3)50;推广:阴影部分的面积为a,应用S△DMQ=700,证明见解析.
试题分析:(1)平行四边形的面积等于底乘以高,设平行四边形ABCD的高为h, △DCM边CD的高也为h,由题
S平行四边形ABCD=CD×h, S△DCM =
 CD×h=
CD×h= S平行四边形ABCD=50;(2)S△DCM=
S平行四边形ABCD=50;(2)S△DCM= CD×h=
CD×h= S平行四边形ABCD=50;(3)S△DCM =
S平行四边形ABCD=50;(3)S△DCM = CD×h=
CD×h= S平行四边形ABCD=50;推广:阴影部分的面积为a,设平行四边形ABCD边AB上的高为h,AD边上的高为H,则S△ADF=
S平行四边形ABCD=50;推广:阴影部分的面积为a,设平行四边形ABCD边AB上的高为h,AD边上的高为H,则S△ADF= AD×H=
AD×H= S平行四边形ABCD=
S平行四边形ABCD= a, S△ABE=
a, S△ABE= AB×h=
AB×h= S平行四边形ABCD=
S平行四边形ABCD= a,故阴影部分的面积=S△ADF+ S△ABE=a;应用:连接OD,由推广的结论,有S△DOM=
a,故阴影部分的面积=S△ADF+ S△ABE=a;应用:连接OD,由推广的结论,有S△DOM= S平行四边形AMOP=150, S△DOQ=
S平行四边形AMOP=150, S△DOQ= S平行四边形OQCN=350, S△MOQ=
S平行四边形OQCN=350, S△MOQ= S平行四边形OMBQ=200,所以S△DMQ=S△DOM+S△DOQ+S△MOQ=150+350+200=700.
S平行四边形OMBQ=200,所以S△DMQ=S△DOM+S△DOQ+S△MOQ=150+350+200=700.试题解析:(1)设平行四边形ABCDCD边上的高为h,则△DCM边CD的高也为h,
∵S平行四边形ABCD=CD×h,
∴S△DCM=
 CD×h=
CD×h= S平行四边形ABCD=50.
S平行四边形ABCD=50.(2)设平行四边形ABCDCD边上的高为h,则△DCM边CD的高也为h,
∵S平行四边形ABCD=CD×h,
∴S△DCM=
 CD×h=
CD×h= S平行四边形ABCD=50.
S平行四边形ABCD=50.(3)设平行四边形ABCDCD边上的高为h,则△DCM边CD的高也为h,
∵S平行四边形ABCD=CD×h,
∴S△DCM=
 CD×h=
CD×h= S平行四边形ABCD=50.
S平行四边形ABCD=50.推广:阴影部分的面积为a,设平行四边形ABCD边AB上的高为h,AD边上的高为H,
则S△ADF=
 AD×H=
AD×H= S平行四边形ABCD=
S平行四边形ABCD= a,
a,S△ABE=
 AB×h=
AB×h= S平行四边形ABCD=
S平行四边形ABCD= a,
a,故阴影部分的面积=S△ADF+S△ABE=a.
应用:连接OD,由推广的结论,有
S△DOM=
 S平行四边形AMOP=150,S△DOQ=
S平行四边形AMOP=150,S△DOQ= S平行四边形OQCN=350,S△MOQ=
S平行四边形OQCN=350,S△MOQ= S平行四边形OMBQ=200,
S平行四边形OMBQ=200,∴S△DMQ=S△DOM+S△DOQ+S△MOQ=150+350+200=700.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


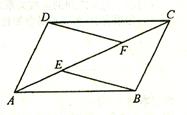
 ABCD的边BC、AD上的点,且BE=DF.
ABCD的边BC、AD上的点,且BE=DF.


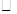 ABCD中,点E、F分别在AB、CD上,且AE=CF.
ABCD中,点E、F分别在AB、CD上,且AE=CF.