Question

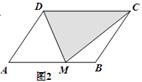
如图，在△ABC中，CD是AB边上的中线，E是CD的中点，过点C作AB的平行线交AE的延长线于F，连结BF.

(1)求证：CF=BD；
(2)若CA=CB，∠ACB=90°，试判断四边形CDBF的形状，并证明你的结论.

Answer 1

（1）详见解析 ;（2）四边形CDBF是正方形，证明详见解析.

试题分析：(1)首先证明△ADE≌△FCE,根据全等三角形的性质得：AD=CF,又AD=BD,所以CF=BD.(2)由（1）知AD=CF,从而得到：CF与DB平行且相等.再根据平行四边形的判定定理得四边形CDBF是平行四边形，再根据等腰三角形“三线合一”的性质，可得：CD=BD,∠CDB=90°,根据“一组邻边相等的平行四边形是菱形”可知CDBF是菱形，再根据“有一个角是直角的平行四边形是矩形”可知四边形CDBF是矩形，所以它是正方形.
试题解析：(1)∵AB∥CF
∴∠EAD=∠EFC, ∠ADE=∠FCE,
∵DE=CE
∴△ADE≌FCE
∴AD=CF
∵AD=BD
∴BD=CF
(2)由（1）知BD=CF
又∵BD∥CF
∴四边形CDBF是平行四边形
∵CA=CB,AD=BD
∴∠CDB=90°,CD=BD=AD
∴四边形CDBF是正方形.