题目内容
在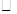
ABCD中，点E、F分别在AB、CD上，且AE=CF．
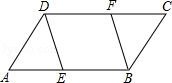
（1）求证：△ADE≌△CBF；
（2）若DF=BF，求证：四边形DEBF为菱形．
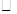ABCD中，点E、F分别在AB、CD上，且AE=CF．（1）求证：△ADE≌△CBF；
（2）若DF=BF，求证：四边形DEBF为菱形．
证明：（1）∵四边形ABCD是平行四边形，∴AD=BC，∠A=∠C，
∵在△ADE和△CBF中，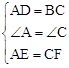
，
∴△ADE≌△CBF（SAS）。
（2）∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD。
∵AE=CF，∴DF=EB。∴四边形DEBF是平行四边形。
又∵DF=FB，∴四边形DEBF为菱形。
∵在△ADE和△CBF中，
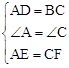，∴△ADE≌△CBF（SAS）。
（2）∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD。
∵AE=CF，∴DF=EB。∴四边形DEBF是平行四边形。
又∵DF=FB，∴四边形DEBF为菱形。
（1）由平行四边形的性质可得AD=BC，∠A=∠C，加上条件AE=CF可利用SAS证明△ADE≌△CBF。
（2）首先证明DF=BE，再加上条件AB∥CD可得四边形DEBF是平行四边形，又DF=FB，可根据邻边相等的平行四边形为菱形证出结论。
（2）首先证明DF=BE，再加上条件AB∥CD可得四边形DEBF是平行四边形，又DF=FB，可根据邻边相等的平行四边形为菱形证出结论。
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
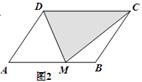
ABCD中，AE⊥BC，垂足为E，CE=CD，点F为CE的中点，点G为CD上的一点，连接DF、EG、AG，∠1=∠2。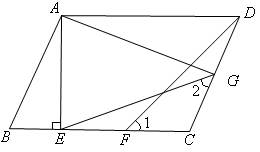
。
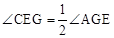≈1.73，
≈1.41，
≈2.24）