题目内容
【题目】如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒.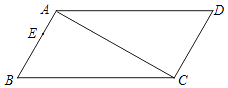
(1)求证四边形ABCD是平行四边形;
(2)当△BEP为等腰三角形时,求t2﹣31t的值;
(3)当t=4时,把△ABP沿直线AP翻折,得到△AFP,求△AFP与ABCD重叠部分的面积.
【答案】
(1)
解:在△ABC和△DCA中  ,
,
∴△ABC≌△DCA(AAS).
∴AB=CD,AD=BC.
∴四边形ABCD是平行四边形
(2)
解:如图1所示:当点P在BC上时.
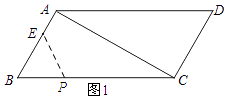
∵△BEP为等腰三角形,∠B=60°,
∴△BEP为等边三角形.
∴BP=BE=3﹣1=2.
∵点P运动的速度为1cm/s,
∴t=2.
∴t2﹣31t=22﹣31×2=﹣58.
如图2所示:当点P在AD上时:EB=EP,作PH⊥AB,PA=15﹣t.
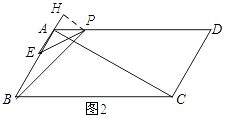
∵∠ABC=60°,AD∥BC,
∴∠HAP=60°.
∵∠H=90°,
∴∠HPA=30°.
∴AH= ![]() AP=
AP= ![]() ,PH=
,PH= ![]() AH=
AH= ![]() .
.
在Rt△EHP中,由勾股定理得:( ![]() +1)2+(
+1)2+( ![]() )2=22,整理得:t2﹣31t=﹣237
)2=22,整理得:t2﹣31t=﹣237
(3)
解:如图所示:设PF与AD交于点M,作MN⊥AP于N,AH⊥BP点H.
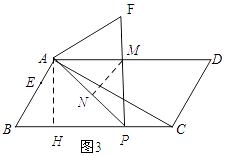
在Rt△ABH中,∠B=60°,则BH= ![]() AB=
AB= ![]() ,AH=
,AH= ![]() .
.
∴HP=4﹣ ![]() =
= ![]() .
.
∴S△APH= ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
在Rt△APH中,依据勾股定理可知AP= ![]() .
.
由翻折的性质可知∠BPA=∠FPA.
∵AD∥BC,
∴∠BPA=∠DAP.
∴∠FPA=∠DAP.
∴AM=PM.
又∵MN⊥AP,
∴AN=NP= ![]() .
.
∵∠AHP=∠MNP=90°,∠BPA=∠FPA,
∴△MPN∽△APH,
∴ ![]() =(
=( ![]() )2=
)2= ![]() .
.
∴S△MNP= ![]() ×
× ![]() =
= ![]() .
.
∵AD∥BC,
∴∠BPA=∠DAP.
∴∠FPA=∠DAP.
∴AM=PM.
又∵MN⊥AP,
∴AN=NP.
∴S△AMP=2S△MNP= ![]()
【解析】(1)首先证明△ABC≌△DCA,依据全等三角形的性质可知AB=CD,AD=BC,接下来,依据两组对边分别相等的四边形是平行四边形进行证明即可;(2)当点P在BC上时,可证明△BEP为等边三角形,从而可求得t=2,将t=2代入所求代数式即可求得代数式的值;当点P在AD上时,作PH⊥AB,PA=15﹣t,在Rt△APH中,∠HAP=60°,于是可求得AH= ![]() ,PH=
,PH= ![]() ,接下来,在Rt△EHP中,由勾股定理可得到关于t的方程,整理这个关于t的方程即可得到问题的答案;(3)设PF与AD交于点M,作MN⊥AP于N,AH⊥BP点H.在Rt△ABH中可求得BH,AH的长,从而可得到HP的长,然后依据勾股定可求得到AP的长,依据三角形的面积可求得S△APH的值,在Rt△APH中,依据勾股定可求得AP=
,接下来,在Rt△EHP中,由勾股定理可得到关于t的方程,整理这个关于t的方程即可得到问题的答案;(3)设PF与AD交于点M,作MN⊥AP于N,AH⊥BP点H.在Rt△ABH中可求得BH,AH的长,从而可得到HP的长,然后依据勾股定可求得到AP的长,依据三角形的面积可求得S△APH的值,在Rt△APH中,依据勾股定可求得AP= ![]() .接下来,证明△AMP为等腰三角形,依据等腰三角形三线合一的性质可得到NP的长,然后证明△MPN∽△APH,依据相似三角形的性质可求得S△MNP的值,最后依据S△AMP=2S△MNP求解即可.
.接下来,证明△AMP为等腰三角形,依据等腰三角形三线合一的性质可得到NP的长,然后证明△MPN∽△APH,依据相似三角形的性质可求得S△MNP的值,最后依据S△AMP=2S△MNP求解即可.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.
时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
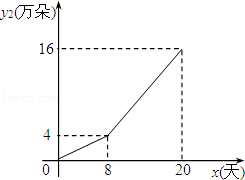
另一部分鲜花在淘宝网销售,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 关系如图所示.
(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律,写出y1与x的函数关系式及自变量x的取值范围;
(2)观察马蹄莲网上销售量y2与时间x的变化规律,请你设想商家采用了何种销售策略使得销售量发生了变化,并写出销售量y2与x的函数关系式及自变量x的取值范围;
(3)设该花木公司日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时最大值.