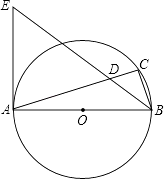
题目内容
【题目】如图,小明在大楼45米高(即PH=45米,且PH⊥HC)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ![]() .(点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上)
.(点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上)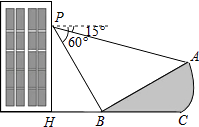
(1)∠PBA的度数等于度;(直接填空)
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732).
≈1.732).
【答案】
(1)90
(2)
解:由题意得:∠PBH=60°,
∵∠ABC=30°,
∴∠ABP=90°,
∴△PAB为直角三角形,
又∵∠APB=45°,
在直角△PHB中,PB=PH÷sin∠PBH=45÷ ![]() =30
=30 ![]() (m).
(m).
在直角△PBA中,AB=PBtan∠BPA=30 ![]() ≈52.0(m).
≈52.0(m).
故A、B两点间的距离约为52.0米
【解析】解:(1)∵山坡的坡度i(即tan∠ABC)为1: ![]() .
.
∴tan∠ABC= ![]() ,
,
∴∠ABC=30°;
∵从P点望山脚B处的俯角60°,
∴∠PBH=60°,
∴∠ABP=180°﹣30°﹣60°=90°
故答案为:90.
(1)根据俯角以及坡度的定义即可求解;(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分: 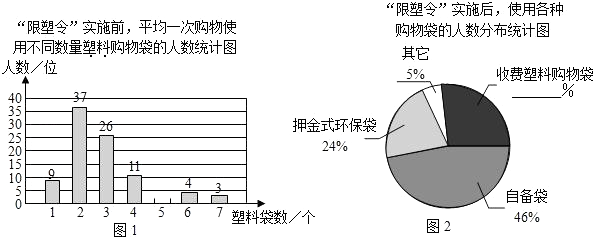
“限塑令”实施后,塑料购物袋使用后的处理方式统计表:
处理方式 | 直接丢弃 | 直接做垃圾袋 | 再次购物使用 | 其它 |
选该项的人数占 | 5% | 35% | 49% | 11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.