题目内容
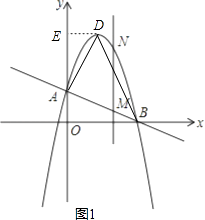
【题目】如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO= ![]() ,抛物线y=﹣x2+bx+c过A、B两点.
,抛物线y=﹣x2+bx+c过A、B两点.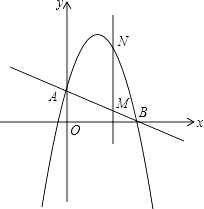
(1)求直线AB和这个抛物线的解析式;
(2)设抛物线的顶点为D,求△ABD的面积;
(3)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN的长度l有最大值?最大值是多少?
【答案】
(1)
解:∵在Rt△AOB中,tan∠ABO= ![]() ,OA=2,
,OA=2,
即 ![]() =
= ![]() ,
,
∴0B=4,
∴A(0,2),B(4,0),
把A、B的坐标代入y=﹣x2+bx+c得: ![]() ,
,
解得:b= ![]() ,
,
∴抛物线的解析式为y=﹣x2+ ![]() x+2,
x+2,
设直线AB的解析式为y=kx+e,把A、B的坐标代入得: ![]() ,
,
解得:k=﹣ ![]() ,e=2,
,e=2,
所以直线AB的解析式是y=﹣ ![]() x+2
x+2
(2)
解:过点D作DE⊥y轴于点E,
由(1)抛物线解析式为y=﹣x2+ ![]() x+2=﹣(x﹣
x+2=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
即D的坐标为( ![]() ,
, ![]() ),
),
则ED= ![]() ,EO=
,EO= ![]() ,
,
AE=EO﹣OA= ![]() ,
,
S△ABD=S梯形DEOB﹣S△DEA﹣S△AOB= ![]() ×(
×( ![]() +4)×
+4)× ![]() ﹣
﹣ ![]() ×
× ![]() ﹣
﹣ ![]() ×4×2=
×4×2= ![]()
(3)
解:由题可知,M、N横坐标均为t.
∵M在直线AB:y=﹣ ![]() x+2上
x+2上
∴M(t,﹣ ![]() t+2)
t+2)
∵N在抛物线y=﹣x2+ ![]() x+2上
x+2上
∴M(t,﹣t2+ ![]() t+2),
t+2),
∵作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N,
∴MN=﹣t2+ ![]() t+2﹣(﹣
t+2﹣(﹣ ![]() +2)=﹣t2+4t=﹣(t﹣2)2+4,
+2)=﹣t2+4t=﹣(t﹣2)2+4,
其中0<t<4,
∴当t=2时,MN最大=4,
所以当t=2时,MN的长度l有最大值,最大值是4
【解析】(1)求出OB,把A、B的坐标代入y=﹣x2+bx+c和y=kx+e求出即可;(2)求出D的坐标,再根据面积公式求出即可;(3)求出M、N的坐标,求出MN的值,再化成顶点式,即可求出答案.

 每课必练系列答案
每课必练系列答案【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分: 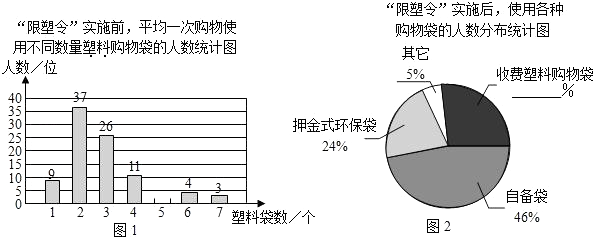
“限塑令”实施后,塑料购物袋使用后的处理方式统计表:
处理方式 | 直接丢弃 | 直接做垃圾袋 | 再次购物使用 | 其它 |
选该项的人数占 | 5% | 35% | 49% | 11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出80m3的部分 | 2.5 |
超出80m3不超出130m3的部分 | a |
超出130m3的部分 | a+0.5 |
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?