��Ŀ����
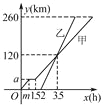
����Ŀ��ij��ľ��˾��20��������һ�������������У��ù�˾���ʻ���������������y1����䣩��ʱ��x��xΪ��������λ���죩���ֶ�Ӧֵ���±���ʾ��
ʱ��x���죩 | 0 | 4 | 8 | 12 | 16 | 20 |
����y1����䣩 | 0 | 16 | 24 | 24 | 16 | 0 |
��һ�����ʻ����Ա������ۣ�����������������y2����䣩��ʱ��x��xΪ��������λ���죩 ��ϵ��ͼ��ʾ��
��1���������ѧ����һ�κ��������κ����ͷ�����������ȷ�����ֺ����ܱ�ʾy1��x�ı仯���ɣ�д��y1��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2���۲�����������������y2��ʱ��x�ı仯���ɣ����������̼Ҳ����˺������۲���ʹ�������������˱仯����д��������y2��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��3����û�ľ��˾����������Ϊy��䣬д��y��ʱ��x�ĺ�����ϵʽ�����жϵڼ�������������y��������ʱ���ֵ�� 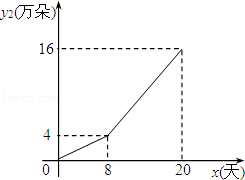
���𰸡�
��1���⣺��ͼ�����ݹ۲��֪y1��x֮���Ƕ��κ�����ϵ��
��y1=ax2+bx+c��a��0����
��  ��
��
��� 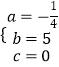 ��
��
��y1��x������ϵʽΪy1=�� ![]() x2+5x��0��x��20��
x2+5x��0��x��20��
��2���⣺����8��û�ľ��˾�����˽��۴����������������ķ����������Ա���ҵ�ע�����������������ӣ�
��0��x��8����y=kx��
�ߺ���ͼ���㣨8��4����
��8k=4��
���k= ![]() ��
��
���ԣ�y= ![]() x��
x��
��8��x��20ʱ����y=mx+n��
�ߺ���ͼ���㣨8��4������20��16����
�� ![]() ��
��
��� ![]() ��
��
���ԣ�y=x��4��
���ϣ�y2= 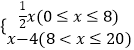 ��
��
��3���⣺��0��x��8ʱ��
y=y1+y2
= ![]() x��
x�� ![]() x2+5x
x2+5x
=�� ![]() ��x2��22x+121��+
��x2��22x+121��+ ![]()
=�� ![]() ��x��11��2+
��x��11��2+ ![]() ��
��
�������߿������£�x��ȡֵ��Χ�ڶԳ�����࣬y��x�����������
�൱x=8ʱ��y�����ֵ��y���=�� ![]() ��8��11��2+
��8��11��2+ ![]() =28��
=28��
��8��x��20ʱ��y=y1+y2=x��4�� ![]() x2+5x��
x2+5x��
=�� ![]() ��x2��24x+144��+32��
��x2��24x+144��+32��
=�� ![]() ��x��12��2+32��
��x��12��2+32��
�������߿������£�������x��ȡֵ��Χ�ڣ�
�൱x=12ʱ��y�����ֵΪ32��
��û�ľ��˾���۵�12�죬����������������ֵΪ32��䣮
����������1�����жϳ�y1��x֮���Ƕ��κ�����ϵ��Ȼ����y1=ax2+bx+c��a��0����Ȼ��ȡ�������ݣ����ô���ϵ��������κ�������ʽ��𣻣�2�����������ӣ��ӽ��۴����Ͽ��ǣ�Ȼ����������ô���ϵ������һ�κ�������ʽ��𣻣�3���֢�0��x��8ʱ����8��x��20ʱ���������������������y=y1+y2 �� �������ٸ��ݶ��κ�������ֵ������

 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ����ʦ����ѧ������ϵ�д�
ͬ����ϰ����ʦ����ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д�