Question

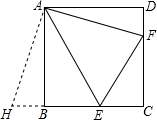
如图正方形ABCD中，点E、F分别在BC、CD上，且∠EAF=45°．
（1）求证：BE+DF=EF；
（2）若BE=3，DF=2，求AB的长．

Answer 1

（1）证明：延长EB至H，使BH=DF，连接AH，
∵在正方形ABCD中，
∴∠ADF=∠ABH，AD=AB，
在△ADF和△ABH中，
∵

AD=AB ∠ADF=∠ABH DF=HB

∴△ADF≌△ABH（SAS），
∴∠BAH=∠DAF，AF=AH，
∴∠FAH=90°，
∴∠EAF=∠EAH=45°，
在△FAE和△HAE中，
∵

AF=AH ∠FAE=∠EAH AE=AE

∴△FAE≌△HAE（SAS），
∴EF=HE=BE+HB，
∴EF=BE+DF，

（2）∵EF=BE+DF，BE=3，DF=2，∴EF=5，
设AB=x，则CE=x-3，CF=x-2，
在△CEF中：FC²+EC²=EF²，
故（x-2）²+（x-3）²=5²，
解得：x₁=-1（舍去），x₂=6，
∴AB=6．