题目内容
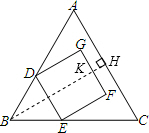
附图为正三角形ABC与正方形DEFG的重叠情形，其中D、E两点分别在AB、BC上，且BD=BE．若AC=18，GF=6，则F点到AC的距离为何？（ ）
| A．2 | B．3 | C．12-4
| D．6
|
如图，过点B作BH⊥AC于H，交GF于K，
∵△ABC是等边三角形，
∴∠A=∠ABC=60°，
∵BD=BE，
∴△BDE是等边三角形，
∴∠BDE=60°，
∴∠A=∠BDE，
∴AC∥DE，
∵四边形DEFG是正方形，GF=6，
∴DE∥GF，
∴AC∥DE∥GF，
∴KH=18×
-6×
-6=9
-3
-6=6
-6，
∴F点到AC的距离为6
-6．
故选D．
∵△ABC是等边三角形，
∴∠A=∠ABC=60°，
∵BD=BE，
∴△BDE是等边三角形，
∴∠BDE=60°，
∴∠A=∠BDE，
∴AC∥DE，
∵四边形DEFG是正方形，GF=6，
∴DE∥GF，
∴AC∥DE∥GF，
∴KH=18×
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
∴F点到AC的距离为6
| 3 |
故选D．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
点P，连接OP，OQ；