题目内容
【题目】如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( ) 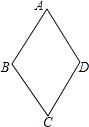
A.52cm
B.40cm
C.39cm
D.26cm
【答案】A
【解析】解:
如图,连接AC、BD相交于点O,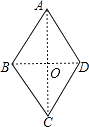
∵四边形ABCD的四边相等,
∴四边形ABCD为菱形,
∴AC⊥BD,S四边形ABCD= ![]() ACBD,
ACBD,
∴ ![]() ×24BD=120,解得BD=10cm,
×24BD=120,解得BD=10cm,
∴OA=12cm,OB=5cm,
在Rt△AOB中,由勾股定理可得AB= ![]() =13(cm),
=13(cm),
∴四边形ABCD的周长=4×13=52(cm),
故选A.
本题主要考查菱形的判定和性质,掌握菱形的面积分式是解题的关键,注意勾股定理的应用.可定四边形ABCD为菱形,连接AC、BD相交于点O,则可求得BD的长,在Rt△AOB中,利用勾股定理可求得AB的长,从而可求得四边形ABCD的周长.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目