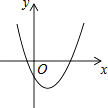题目内容
【题目】如图，已知抛物线y=﹣x2+mx+m﹣4经过点A（5，﹣5），若抛物线顶点为P．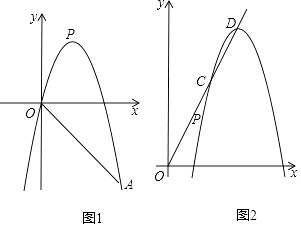
（1）求点P的坐标；
（2）在直线OA上方的抛物线上任取一点M，连接MO、MA，求△MOA的面积取得最大时的点M坐标；
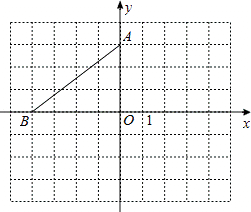
（3）如图1，将原抛物线沿射线OP方向进行平移得到新的抛物线，新抛物线与射线OP交于C、D两点．试问线段CD的长度是否为定值，若是请求出这个定值；若不是请说明理由．（提示：若点C（x1 ， y1），D（x2 ， y2），则CD的长度d= 
）
【答案】
（1）
解：依题意﹣52+5m+m﹣4=﹣5，
∴m=4，
∴y=﹣x2+4x=﹣（x﹣2）2+4
∴顶点P（2，4）
（2）
解：如图1，
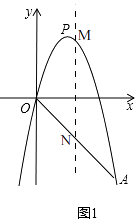
∵A（5，﹣5），
∴OA的解析式为y=﹣x，
设M（m，﹣m2+4m），（0＜m＜5）
∴N（m，﹣m），
∴MN=﹣m2+4m+m=﹣m2+5m，
∴S△MOA= 
MN|xA﹣xO|= （﹣m2+5m）5=﹣ 
（m2﹣5m）=﹣ （m﹣ ）2+ 
∴当m= 时，△MOA的面积取得最大，此时的点M坐标（ ， 
）
（3）
解：在抛物线平移的过程中，线段CD的长度是为定值，
∵直线OP的解析式为y=2x，
∴可设新抛物线解析式为y=﹣（x﹣a）2+2a
联立抛物线与OP，
，
∴﹣（x﹣a）2﹣ 
a=﹣ x，
∴x1=a，x2=a﹣2，x1﹣x2=2；
y1=2x1=2a，y2=2x2=2（a﹣2），y1﹣y2=4；
∴CD的长度= 
= 
=2 
∴在抛物线平移的过程中，线段CD的长度是定值，定值为2
【解析】（1）根据待定系数法，可得函数解析式，根据配方法，可得顶点坐标；（2）先设出点M坐标，得出三角形MOA面积，进而确定出点M的坐标．（3）根据平移规律，可得新抛物线，根据联立抛物线与OP，可得C、D点的横坐标，根据勾股定理，可得答案．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
