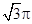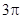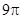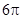题目内容
⊙O的半径为1,AB是⊙O 的一条弦,且AB=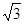 ,则弦AB所对的弧长为_________
,则弦AB所对的弧长为_________
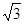 ,则弦AB所对的弧长为_________
,则弦AB所对的弧长为_________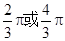
弦AB所对的圆心角有两个,先计算出弦AB所对的小圆心角为120°,求得劣弧的长,再求所对的优弧的长.
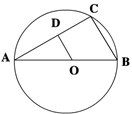
解:过点O作OC⊥AB于点C,
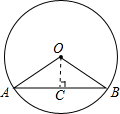
∵OA=1,AC=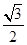 ,由勾股定理得,OC=
,由勾股定理得,OC=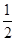 ,根据三角函数的定义,sin∠AOC=
,根据三角函数的定义,sin∠AOC=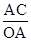 ,即sin∠AOC=
,即sin∠AOC=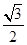 ,
,
∴∠AOC=60°,∠AOB=120°,
由弧长公式得:劣弧=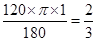 π,优弧=
π,优弧=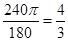 π.
π.
解:过点O作OC⊥AB于点C,

∵OA=1,AC=
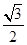 ,由勾股定理得,OC=
,由勾股定理得,OC=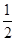 ,根据三角函数的定义,sin∠AOC=
,根据三角函数的定义,sin∠AOC=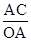 ,即sin∠AOC=
,即sin∠AOC=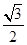 ,
,∴∠AOC=60°,∠AOB=120°,
由弧长公式得:劣弧=
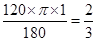 π,优弧=
π,优弧=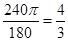 π.
π.
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
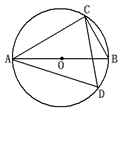
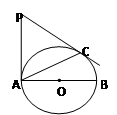
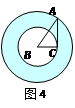
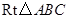 中,
中,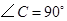 ,
,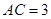 .将其绕
.将其绕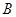 点顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环.该圆环的面积为
点顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环.该圆环的面积为