题目内容
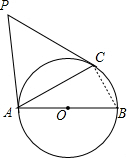
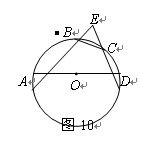
已知AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
小题1:求∠P的度数;
小题2:若AB=2,求PA的长.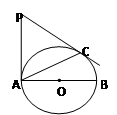
小题1:求∠P的度数;
小题2:若AB=2,求PA的长.
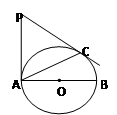
小题1:∠P=60°;(
小题2:PA=

(Ⅰ)根据切线的性质及切线长定理可证明△PAC为等边三角形,则∠P的大小可求;
(Ⅱ)由(Ⅰ)知PA=PC,在Rt△ACB中,利用30°的特殊角度可求得AC的长.
解:(Ⅰ)∵PA是⊙O的切线,AB为⊙O的直径,
∴PA⊥AB,
∴∠BAP=90°;
∵∠BAC=30°,
∴∠CAP=90°-∠BAC=60°.
又∵PA、PC切⊙O于点A、C,
∴PA=PC,
∴△PAC为等边三角形,
∴∠P=60°.
(Ⅱ)如图,连接BC,则∠ACB=90°.
在Rt△ACB中,AB=2,∠BAC=30°,


练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 与⊙O
与⊙O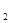 外切,⊙O
外切,⊙O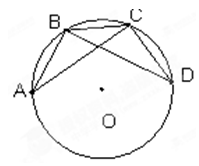
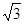 ,则弦AB所对的弧长为_________
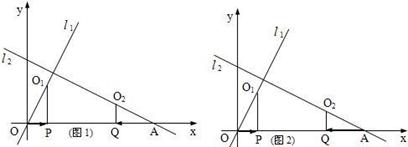
,则弦AB所对的弧长为_________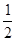 x+4(即直线l2),l2与x轴相交于点A.点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位.设运动了t秒.
x+4(即直线l2),l2与x轴相交于点A.点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位.设运动了t秒.