Question

【题目】已知：⊙O1与⊙O2相交于A、B两点，且O2在⊙O1上．

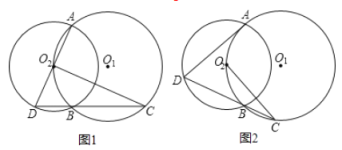
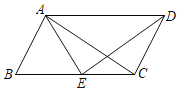
（1）如图1，AD是⊙O2的直径，连DB并延长交⊙O1于点C，求证：CO2⊥AD．

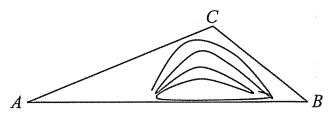
（2）如图2，若AD是⊙O2的非直径的弦，直线DB交⊙O1于点C，则(1)中的结论是否成立，为什么？请加以证明．

Answer 1

【答案】（1）见解析；（2）见解析．

【解析】

(1) 连接AB．根据直径所对的圆周角是直角，得∠ABD=90°；根据等弧所对的圆周角相等，得∠A=∠C，再进一步根据两角对应相等，得△ABD∽△CO2D，从而证明结论；
(2) 连接AO2并延长交圆于E，连接DE、AB．根据直径所对的圆周角是直角，得∠ADE=90°；根据等弧所对的圆周角相等，得∠C=∠1=∠2，从而证明∠ADC+∠C=90°，证明结论．

(1) 连结AB，如图1

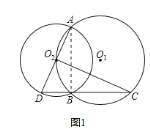
∵AD是⊙O2的直径，

∴∠ABD＝90°（直径所对的圆周角是直角），

∴∠BAD＋∠BDA＝180°-90°=90°（三角形内角和定理），

又∵∠C＝∠A（同弧所对圆周角相等），

∴△ABD∽△CO2D，
∴∠ABD=∠CO2D=90°，
即CO2⊥AD．

(2)(1)中的结论仍成立．证明如下：

连接AO2并延长交圆于E，延长CO2交AD于H，连接DE、AB，如图2

∵AE是圆的直径，
∴∠ADE=90°（直径所对的圆周角是直角），

∴∠ADC+∠2=90°，
又∵∠C=∠1=∠2（同弧所对圆周角相等），
∴∠ADC+∠C=90°（等量替换），

∴∠AHD=180°-90°=90°（三角形内角和定理），
则CO2⊥AD．