题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
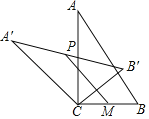
A.4B.3C.2D.1
【答案】B
【解析】
连接PC,根据∠A=30°,BC=2,可知AB的值,根据旋转的性质可知A′B′=AB,进而可知A′P、PB′、PC的知,结合图形和三角形三边关系即可得出PM的取值范围,进而可知P、C、M共线时,PM值最大,即可选出答案.
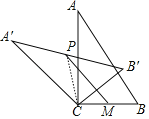
解:如图连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4,
根据旋转不变性可知,A′B′=AB=4,
∴A′P=PB′,
∴PC=![]() A′B′=2,
A′B′=2,
∵CM=BM=1,
又∵PM≤PC+CM,即PM≤3,
∴PM的最大值为3(此时P、C、M共线).
故选:B.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
【题目】目前节能灯在城市已基本普及,为响应号召,某商场计划购进甲,乙两种节能灯共200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 | 20 | 30 |
乙型 | 30 | 45 |
(1)若购进甲,乙两种节能灯共用去5200元,求甲、乙两种节能灯各进多少只?
(2)若商场准备用不多于5400元购进这两种节能灯,问甲型号的节能灯至少进多少只?
(3)在(2)的条件下,该商场销售完200只节能灯后能否实现盈利超过2690元的目标?若能请你给出相应的采购方案;若不能说明理由.