题目内容
【题目】已知在矩形ABCD中,AB=4,AD=3,⊙C与对角线BD相切.
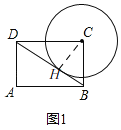
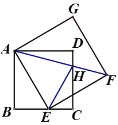
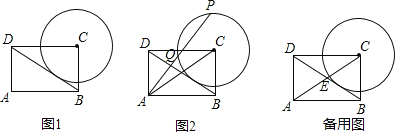
(1)如图1,求⊙C的半径;
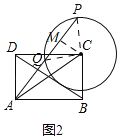
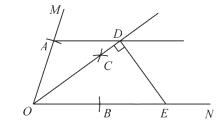
(2)如图2,点P是⊙C上一个动点,连接AP,AC,AP交⊙C于点Q,若sin∠PAC=![]() ,求∠CPA的度数和弧PQ的长;
,求∠CPA的度数和弧PQ的长;
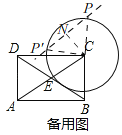
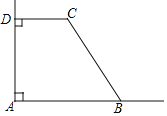
(3)如图,对角线AC与⊙C交于点E,点P是⊙C上一个动点,设点P到直线AC的距离为d,当0<d≤![]() 时,请直接写出∠PCE度数的取值范围.
时,请直接写出∠PCE度数的取值范围.
【答案】(1)![]() ;(2)60°,
;(2)60°,![]() ;(3)0°<∠PCE≤60°或120°≤∠PCE<180°
;(3)0°<∠PCE≤60°或120°≤∠PCE<180°
【解析】
(1)先利用勾股定理求出BD,再用三角形的面积公式求解即可得出结论;
(2)先根据三角函数求出CM和∠CPM,进而求出∠PCQ,最后用弧长公式计算即可得出结论;
(3)先判断出0<CN≤![]() ,再利用三角函数求出分界点CN=
,再利用三角函数求出分界点CN=![]() 时的∠PCE的度数,即可得出结论.
时的∠PCE的度数,即可得出结论.
(1)如图1,在矩形ABCD中,CD=AB=4,BC=AD=3,∠BCD=90°,
设切点为H.连接CH,
∵ BD与⊙C相切于H,
∴ CH⊥BD,
根据勾股定理得,BD=![]() ,
,
∵ S△BCD=![]() BCCD=
BCCD=![]() BDCH,
BDCH,
∴ CH=![]() ,
,
即⊙C的半径为![]() ;
;
(2)如图2,连接CP,CQ,过点C作CM⊥AP于M,
∵ 四边形ABCD是矩形,
∴ AC=BD=5,
在Rt△ACM中,sin∠PAC=![]() ,
,
∴ CM=![]() ,
,
在Rt△CMP中,sin∠CPM=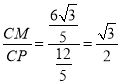 ,
,
∴∠CPM=60°,
即∠CPA=60°,
∵ CP=CQ,
∴ △CPQ是等边三角形,
∴ ∠ PCQ=60°,
∴ 弧PQ的长为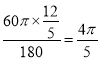 ;
;
(3)如图备用图,过点P作PP'∥AC,过点C作CN⊥PP'于N,
则∠PCN=∠P'CN,∠ECN=∠CNP=90°,
∴ 点P到AC的距离d=CN,
∵ 0<d≤![]() ,
,
∴ 0<CN≤![]() ,
,
当CN=0时,点P在直线AC上,∠PCE=0°,
当CN=![]() 时,连接CP,CP',
时,连接CP,CP',
在Rt△P'CN中,cos∠P'CN=![]() =
=![]() =
=![]() ,
,
∴ ∠P'CN=30°,
∴ ∠PCN=∠P'CN=30°
∴ ∠P'CE=∠ECN﹣∠P'CN=60°,∠PCE=∠ECN+∠PCN=120°,
∴ ∠PCE度数的取值范围为0°<∠PCE≤60°或120°≤∠PCE<180°