题目内容
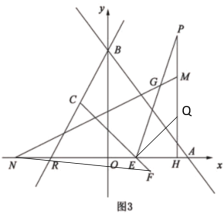
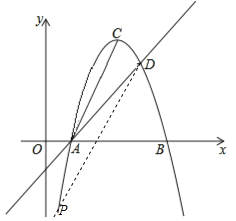
【题目】如图,直线y=x﹣1与抛物线y=﹣x2+6x﹣5相交于A、D两点.抛物线的顶点为C,连结AC.
(1)求A,D两点的坐标;
(2)点P为该抛物线上一动点(与点A、D不重合),连接PA、PD.
①当点P的横坐标为2时,求△PAD的面积;
②当∠PDA=∠CAD时,直接写出点P的坐标.
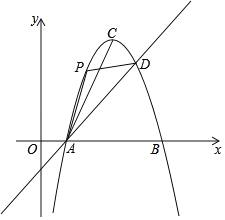
【答案】(1)A(1,0),D(4,3);(2)①当点P的横坐标为2时,求△PAD的面积;②当∠PDA=∠CAD时,直接写出点P的坐标.
【解析】
(1)由于A、D是直线直线y=x﹣1与抛物线y=﹣x2+6x﹣5的交点,要求两个交点的坐标,需可联立方程组求解;
(2)①要求△PAD的面积,可以过P作PE⊥x轴,与AD相交于点E,求得PE,再用△PAE和△PDE的面积和求得结果;
②分两种情况解答:过D点作DP∥AC,与抛物线交于点P,求出AC的解析式,进而得PD的解析式,再解PD的解析式与抛物线的解析式联立方程组,便可求得P点坐标;当P点在AD上方时,延长DP与y轴交于F点,过F点作FG∥AC与AD交于点G,则∠CAD=∠FGD=∠PDA,则FG=FD,设F点坐标为(0,m),求出G点的坐标(用m表示),再由FG=FD,列出m的方程,便可求得F点坐标,从而求出DF的解析式,最后解DF的解析式与抛物线的解析式联立的方程组,便可求得P点坐标.
(1)联立方程组![]() ,
,
解得,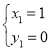 ,
,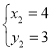 ,
,
∴A(1,0),D(4,3),
(2)①过P作PE⊥x轴,与AD相交于点E,
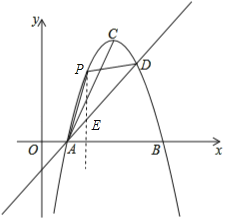
∵点P的横坐标为2,
∴P(2,3),E(2,1),
∴PE=3﹣1=2,
∴![]() =3;
=3;
②过点D作DP∥AC,与抛物线交于点P,则∠PDA=∠CAD,
∵y=-x2+6x-5=-(x-3)2+4,
∴C(3,4),
设AC的解析式为:y=kx+b(k≠0),
∵A(1,0),
∴![]() ,
,
∴![]() ,
,
∴AC的解析式为:y=2x-2,
设DP的解析式为:y=2x+n,
把D(4,3)代入,得3=8+n,
∴n=-5,
∴DP的解析式为:y=2x-5,
联立方程组![]() ,
,
解得,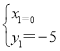 ,
,![]() ,
,
∴此时P(0,-5),
当P点在直线AD上方时,延长DP,与y轴交于点F,过F作FG∥AC,FG与AD交于点G,
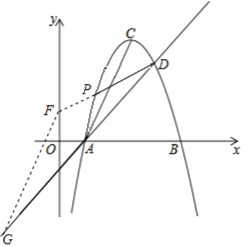
则∠FGD=∠CAD=∠PDA,
∴FG=FD,
设F(0,m),
∵AC的解析式为:y=2x-2,
∴FG的解析式为:y=2x+m,
联立方程组![]() ,
,
解得,![]() ,
,
∴G(-m-1,-m-2),
∴FG=![]() ,FD=
,FD=![]() ,
,
∵FG=FD,
∴![]() =
=![]() ,
,
∴m=-5或1,
∵F在AD上方,
∴m>-1,
∴m=1,
∴F(0,1),
设DF的解析式为:y=qx+1(q≠0),
把D(4,3)代入,得4q+1=3,
∴q=![]() ,
,
∴DF的解析式为:y=![]() x+1,
x+1,
联立方程组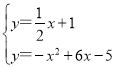
∴![]() ,
,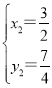 ,
,
∴此时P点的坐标为(![]() ,
,![]() ),
),
综上,P点的坐标为(0,-5)或(![]() ,
,![]() ).
).

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案【题目】小西红柿又叫圣女果,既可以生吃,也可以作为美食原料,营养价值极高,因此深受人们的欢迎,为了解甲、乙两个规模相当的种植基地的小西红柿产量,从这两个种植基地中各随机选取50株小西红柿秧苗进行调查,将得到的数据分类整理成如下统计表:
甲基地每株秧苗收获小西红柿个数统计表:
小西红柿个数x/个 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
秧苗株数/株 | 4 | 8 | 12 | 12 | 10 | 4 |
乙基地每株秧苗收获小西红柿个数统计表:
小西红柿个数 x/个 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
秧苗株数/株 | 9 | 6 | 12 | 10 | 11 | 2 |
(说明:x<45为产量不合格,x≥45为产量合格,其中45≤x<65为产量良好,65≤x<85为产量优秀)
(
(2)某水果商准备在甲、乙两个小西红柿种植基地中选择一个进行合作,若一株秧苗产量优秀可获利13元,产量良好可获利8元,产量不合格亏损5元.以这两个基地的50株秧苗获得的平均利润为决策依据,请你利用所学的统计知识帮该水果商选择与哪个基地进行合作能获得更大利润?并说明理由.
【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
(1)(收集数据)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是________.
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
(2)(整理数据)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
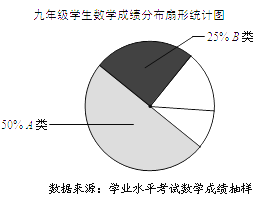
①C类和D类部分的圆心角度数分别为________°、________°;
②估计九年级A、B类学生一共有________名.
(3)(分析数据)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.