Question

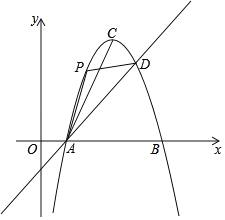
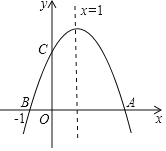
【题目】在平面直角坐标系中，直线交轴于点，交轴于点，．

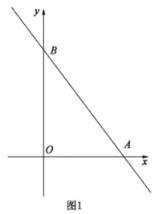
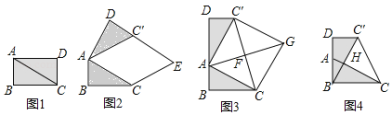
（1）如图1，求的值；

（2）如图2，经过点的直线与直线交于点，与轴交于点，，交于点，设线段长为，求与的函数关系式；

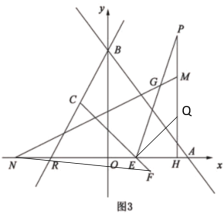
（3）如图3，在（2）的条件下，点在第四象限，交于点，,点在第一象限，，点在轴上，点在上，交于点，，过点作，交于点， ，，，点的坐标为，连接，求的面积．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）先用b表示出点B和点A的坐标，然后利用勾股定理列出方程即可求出b的值；

（2）联立直线BC的解析式和直线AB的解析式即可用n表示出点C的坐标，从而求出点D的坐标，从而求出与的函数关系式；

（3）过点C作CS⊥x轴于S，过点F作FT⊥x轴于T，过点G作GD⊥y轴于D，MN与y轴交于点I，根据相似三角形判定可得△RSC∽△ROB，列出比例式即可求出OR和CS，然后根据等角的锐角三角函数相等求出ON，再根据等腰直角三角形的性质求出NE，然后结合已知条件和等角的锐角三角函数相等求出TF，即可求出结论．

解：（1）当x=0时，y=b；当y=0时，x=

∴点B的坐标为（0，b），点A的坐标为（，0）

∴OB=b，OA=

根据勾股定理OB2＋OA2=AB2

b 2＋（）2=102

解得：b=8或-8（不符合已知条件，舍去）

∴b=8

（2）直线BC的解析式为，直线AB的解析式为

联立

解得：

∴点C的坐标为（-2，-2n）

∵

∴点D的纵坐标为-2n

将y=-2n代入中，解得：x=

∴点D的坐标为

∴线段长=－（-2）=

（3）过点C作CS⊥x轴于S，过点F作FT⊥x轴于T，过点G作GD⊥y轴于D，MN与y轴交于点I

∴OD=，GD=

由（2）知点C坐标为（-2，-2n）

∴CS=-2n，OS=2

∵，CS∥y轴

∴RB=2RC，△RSC∽△ROB

∴

即

解得：n=-2，OR=4

∴CS=4

∵，GD∥x轴

∴=∠DGI

∴=tan∠DGI

∴

即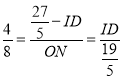

解得：

∵

∴∠CES=∠AEF=45°，∠QEH=∠QEF－∠AEF=45°

∴△CES、△EFT和△EHQ都是等腰直角三角形

∴CS=SE=4，ET=TF=， EH=HQ，设EH=HQ=a，则EQ=

∴EN=ON＋OE=ON＋SE－OS=9

∵，

∴EF=，PM=a，PH=9，

∴NH=EN＋EH=9＋a，MH=PH－PM=9－a

∴=

∴

解得：a=3

∴EF=

∴TF=

∴S△EFN=EN·TF=×9×1=