题目内容
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.
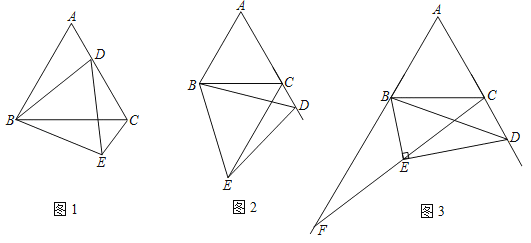
(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
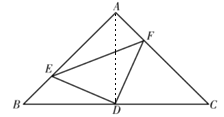
(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.

【答案】(1)见解析;(2)见解析
【解析】
(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
(2)根据题意画出图形,连接AD,构造△DAF≌△DBE.得出FD=ED ,∠FDA=∠EDB,再算出∠EDF=90°,即可得出△DEF是等腰直角三角形.
解:(1)连结AD ,
∵AB=AC ,∠BAC=90° ,D为BC中点 ,
∴AD⊥BC ,BD=AD ,
∴∠B=∠BAD=∠DAC=45°,
又∵BE=AF ,
∴△BDE≌△ADF(SAS),
∴ED=FD ,∠BDE=∠ADF,
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,
∴△DEF为等腰直角三角形.
(2)连结AD
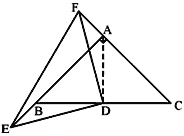
∵AB=AC ,∠BAC=90° ,D为BC中点 ,
∴AD=BD ,AD⊥BC ,
∴∠DAC=∠ABD=45° ,
∴∠DAF=∠DBE=135°,
又∵AF=BE ,
∴△DAF≌△DBE(SAS),
∴FD=ED ,∠FDA=∠EDB,
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF为等腰直角三角形.