题目内容
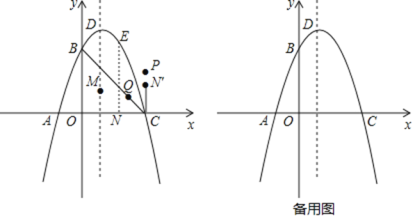
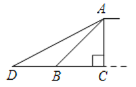
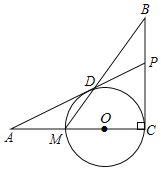
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是⊙O的切线;
(3)若AD=12,AM=MC,求PB和DM的值.
【答案】(1)见解析;(2)见解析;(3)PB=6,DM=2![]() .
.
【解析】
(1)根据两边对应成比例,且夹角相等的两三角形相似证明即可.
(2)首先证明△ODP≌△OCP(SAS),可得∠ODP=∠OCP,则∠ODP=90°,证出OD⊥PA即可解决问题.
(3)连接CD.由(1)可知:PC=PD,由AM=MC,推出AM=2MO=2R,在Rt△AOD中,OD2+AD2=OA2,可得R2+122=9R2,推出R=3![]() ,推出OD=3
,推出OD=3![]() ,MC=6
,MC=6![]() ,由
,由![]() ,可得DP的长度,再根据中点及勾股定理求出MB的长度,最后利用相似三角形的性质求出DM即可解决问题.
,可得DP的长度,再根据中点及勾股定理求出MB的长度,最后利用相似三角形的性质求出DM即可解决问题.
(1)证明:连接OD、OP、CD.
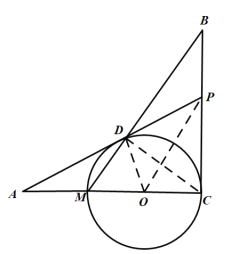
∵ADAO=AMAP,
∴![]() ,∠A=∠A,
,∠A=∠A,
∴△ADM∽△APO.
(2)证明:∵△ADM∽△APO,
∴∠ADM=∠APO,
∴MD![]() PO,
PO,
∴∠DOP=∠MDO,∠POC=∠DMO,
∵OD=OM,
∴∠DMO=∠MDO,
∴∠DOP=∠POC,
∵OP=OP,OD=OC,
∴△ODP≌△OCP(SAS),
∴∠ODP=∠OCP,
∵BC⊥AC,
∴∠ODP=∠OCP=90°,
∴OD⊥AP,
∴PD是⊙O的切线.
(3)解:连接OD、OP、CD,设圆的半径为R,
∵△ODP≌△OCP
∴PC=PD,
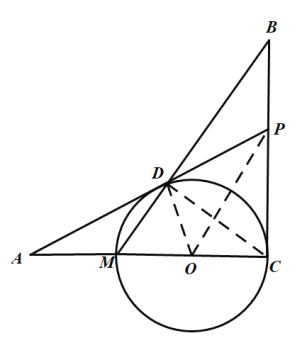
∵AM=MC,
∴AM=2MO=2R,
在Rt△AOD中,OD2+AD2=OA2,
∴R2+122=9R2,
∴R=3![]() ,
,
∴OD=3![]() ,MC=6
,MC=6![]() ,
,
∵![]()
∴![]() ,
,
∴AP=18,
∴DP=AP﹣AD=18﹣12=6,
∵O是MC的中点,MB![]() PO,
PO,
∴![]() ,
,
∴点P是BC的中点,
∴PB=CP=DP=6,
∵MC是⊙O的直径,
∴∠BDC=∠CDM=90°,
在Rt△BCM中,
∵BC=2DP=12,MC=6![]() ,
,
∴BM=![]() =
=![]() =6
=6![]() ,
,
∵![]() ,
,
∴△BCM∽△CDM,
∴![]() ,即
,即![]() ,
,
∴DM=2![]() .
.

【题目】某公司计划投资![]() 万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为
万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为![]() 件,每件总成本为
件,每件总成本为![]() 万元,每件出厂价
万元,每件出厂价![]() 万元;流水生产线投产后,从第
万元;流水生产线投产后,从第![]() 年到第
年到第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)如下表:
(万元)如下表:
第 |
|
|
|
|
|
| ··· |
维修、保养费用累计 |
|
|
|
|
|
| ··· |
若上表中第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)与
(万元)与![]() 的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)投产第几年该公司可收回![]() 万元的投资?
万元的投资?
(3)投产多少年后,该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)?